ХАОС И СЛОЖНОСТЬ В ЧИСТОЙ МАТЕМАТИКЕ

Международный Журнал Бифуркации и Хаоса
(International Journal of Bifurcation and Chaos)
Vol. 4, No. 1, February 1994
Грегори Чейтин
G.J. chaitin
IBM Research Division
P.O. Box 704
Yorktown Heights, NY 10598, USA
chaitin@watson.ibm.com
Лекция прочитана в четверг, 22 февраля 1992 года в Колледже Математики и Информатики университета в Нью-Мехико (Mathematics - Computer Science Colloquium at the University of New Mexico). На лекции делалась видеосъемка. Ниже представлена отредактированная стенограмма. Лекция первоначально издана под названием "Хаотичность в арифметике и крушение редукционизма в чистой математике" ("Randomness in arithmetic and the decline and fall of reductionism in pure mathematics") в июне 1993 г. в бюллетене European Association for Theoretical Computer Science.
К русскому переводу.
Перевод лекции на русский язык любительский, может содержать неточности и явные ошибки. Поэтому рекомендуется рассматривать данный текст как ознакомительный. Для более глубокого изучения вопроса следует найти первоисточник.
A.Семенов

Резюме
Общепринято думать, что всякая истина имеет причину. Я нашел математические истины, которые не имеют никакой причины вообще. Эти математические истины неподвластны математическим рассуждениям, потому что они беспричинны и случайны.
Используя программное обеспечение Mathematica, которая выполняется на рабочей станции IBM/6000 я построил громоздкое алгебраическое уравнение на 200-х страницах с параметром N и 17 000 неизвестными.
левая часть уравнения (N) = правая часть уравнения (N)
Спрашивается для каждого целочисленного параметра N, имеет ли это уравнение конечное или бесконечное число решений в целых числах? Ответ не подчиняется математической причинности, потому что он полностью хаотичен и случаен. Эта работа продолжение известного результатов Геделя и Тьюринга, но использует идеи из новой области называемой теорией алгоритмической информации.
1. Гильберт и аксиоматический метод
Месяц назад я присутствовал на симпозиуме по редукционизму, проходившей в Кембриджском Университете, в котором Тьюринг сделал свою знаменитую работу. Я хотел бы повторить высказанные мной там, и рассказать, как моя работа продолжает и расширяет идеи Тьюринга.
Два предыдущих докладчика высказались не очень лестные о Давиде Гильберте. И я мог бы начать с утверждения, что вопреки тому, что я услышал, Гильберт не заслуживает упреков!
Идеи Гильберта - это кульминация двух тысячелетней математической традиции, начиная с аксиоматического устрожения геометрии Евклидом, через мечту Лейбница о символической логике и все это венчается монументальным трудом "Принцип Математики" Рассела и Уайтхеда (Principia Mathematica). Гильберт мечтал раз всегда разъяснить методы математического рассуждения.
Он мечтал выстроить формальную аксиоматическую систему, которая охватит всю математику.
Формальная Аксиоматическая Система
---- >
---- >
---- >
Гильберт выделял ряд ключевых свойств, которыми такая аксиоматическая система должна обладать. Она должна быть подобно компьютерному языку программирования. В ней точно установлены методы рассуждений, которые, с помощью аксиом и методов вывода порождают ту кажущуюся хаотичность и сложность в чистой математики, которую мы воспринимаем как математики. Кроме того, Гильберт предлагал, что формальная аксиоматическая система, которую он надеялся выстроить, система которая охватывает всю математику, должна быть непротиворечивой (последовательной) и, кроме того, полной.
Формальная Аксиоматическая Система
---- > Непротиворечивость
---- > Полнота
---- >
Последовательность означает, что методы системы не допускают внутри нее одновременного доказательства некого утверждения и противоположного ему, то есть его отрицания.
Формальная Аксиоматическая Система
---- > Непротиворечивость A ~A
{ для всякого A истинно ~ (A /\ ~A) прим А.С.}
---- > Полнота
---- >
Вы не должны быть способны доказать A и ~A (не A). Это было бы крайне нежелательно.
Полнота означает, что если вы делаете осмысленное утверждение, то вы должны быть способны разрешить его тем или иным образом. Либо подтвердить его, либо опровергнуть. Это означает что возможно одно из двух. Либо А, либо не-A непременно должно быть теоремой, доказуемой из аксиом по правилам вывода внутри формальной аксиоматической системы.
Формальная Аксиоматическая Система
---- > Непротиворечивость A ~A
---- > Полнота A ~A
{ для всякого A истинно (A \/ ~A) прим А.С. }
---- >
Рассмотрим любое осмысленное утверждение A и его противоположность не A. Тогда ровно одно из них должно быть доказуемо, если формальная аксиоматическая система непротиворечива и полна.
Формальная аксиоматическая система подобна языку программирования. Имеется алфавит, правила грамматики и другие символы формального синтаксиса. Именно с такого рода вещами мы хорошо знакомы теперь. Разыщите "Принципы Математики" Рассела и Уайтхеда и вы обнаружите, что это три огромных тома битком набитых символами и у вас возникнет ощущение, что вы смотрите в листинг огромной компьютерной программы на некотором непостижимом языке программирования.
Теперь рассмотрим крайне удивительный факт. Непротиворечивость и полнота предполагает исключительно только истину и абсолютно всю истину. И это похоже на разумные требования.
Но, тем не менее, обнаруживается забавный вывод по поводу того, что называется проблемой разрешимости. На немецком - Entscheidungsproblem
Формальная Аксиоматическая Система
---- > Непротиворечивость A ~A
---- > Полнота A ~A
---- > Проблема разрешимости
Гильберт сделал важный шаг в связи с проблемой разрешимости.
Развязать проблему разрешимости для формальной аксиоматической системы может алгоритм, который позволяет вам решить является ли любое данное осмысленное утверждение теоремой или нет? Такой алгоритм называется разрешающей процедурой.
ГИЛЬБЕРТ
Формальная Аксиоматическая Система
---- > Непротиворечивость A ~A
---- > Полнота A ~A
---- > Разрешающая процедура
Это звучит сверхъестественно. Формальная аксиоматическая система, которую хотел выстроить Гильберт, будет включать всю математику: элементарную арифметику, исчисления, алгебру, все!
И если существует разрешающая процедура, то математики остались без работы! Эта разрешающая процедура может проверять является ли какое-либо утверждение теоремой или нет, она может проверять является ли оно истинным или нет. В таком контексте требование, чтобы существовала такая разрешающая процедура для такой формальной системы, выглядит как требование чего-то слишком многого!
Однако легко видеть, что если система непротиворечива и полна, что подразумевалось само собой, то разрешающая процедура должна существовать! Для этого вы должны иметь формальный язык с конечным алфавитом и грамматику.
И Гильберт подчеркивал, как отдельный пункт свойств формальной аксиоматической системы, что должна иметься механическая процедура для проверки того является ли предполагаемое доказательство правильным или нет, удовлетворяет ли оно установленным правилам или нет. Это предполагало, что математическая истина, если быть объективным, такова что каждый мог согласиться следует ли доказательство из правил или нет.
И так, если все это имеет место быть, то вы пробегаете все возможные утверждения в порядке их длинны и смотрите на все последовательности из символов алфавита длинной в один знак, два знака, три знака… тысяча, тысяча один знак… в сотню тысяч символов длинной… К каждому вы применяете механическую процедуру, которая является сущностью формальной аксиоматической системы, и тем самым проверяете имеет ли каждое из этих утверждение силу или нет. По большей части все эти утверждения будут, естественно, ерундой, они будет грамматически неверны. Но вы в конечном итоге найдете каждое и возможных доказательств. Это подобно миллиону непрерывно печатающих обезьян. Рано или поздно вы найдете каждое возможное доказательство. Но это только в принципе. Количество вариантов растет по экспоненте, и поэтому вы не можете организовать сколько-нибудь серьезный перебор на практике. Вы никогда бы не добрались бы до доказательства длинной в одну страницу.
Но теоретически вы можете получить все возможные доказательства, проверять какие из них имеют силу, вникать в то, что они доказывают, и это тот путь, которым вы можете систематически находить все возможные теоремы. Другими словами, имеется алгоритм, механическая процедура, для производства одной за другой каждой теоремы, которая может появиться в формальной аксиоматической системе. Так если для каждого осмысленного утверждения в пределах системы существует либо соответствующая ему теорема либо ее отрицающая и только одна из них (теорема интерпретируется как данное утверждение или его отрицание А.С ), то вы получите разрешающую процедуру. Чтобы узнать является ли некое утверждение теоремой или нет, вы "всего лишь" пробегаете все возможные доказательства, пока не найдете теорему, интерпретируемую как данное утверждение, либо вы натыкаетесь на теорему, интерпретируемую как противоположную искомой.
Отсюда кажется, что Гильберт на самом деле намеревался решить раз и навсегда все математические проблемы. Это звучит удивительно, но, по всей видимости, так это и было. Он полагал, что будет способен выстроить непротиворечивую и полную формальную аксиоматическую систему для всей математики и в результате этого получит разрешающую процедуру для всей математики. Это то к чему пришла формально-аксиоматическая традиция в математике.
Но я уверен, что Гильберт не надеялся получить практически полезную разрешающую процедуру. Та, которую я видел, могла бы работать только в принципе. Она экспоненциально медленная, просто ужасно медленная! Она абсолютно не применима на практике! Но идея состояла в том, что если бы все математики могли согласиться с тем, что является правильным доказательством, что система последовательна и полна, то в принципе это дало бы разрешающую процедуру для автоматического решения любой математической проблемы. Это была великая мечта Гильберта, и ее реализация должна была стать кульминацией идей Евклида, Лейбница, Буля, Пеано, Рассела и Уайтхеда. Единственной проблемой, вставшей на пути к воплощению этого вдохновенного проекта, оказалось то, что эта мечта, как выяснилось, не выполнима!
2. Гедель, Тьюринг и диагональный процесс Кантора
Гильберт действительно вдохновлял. Известна его лекция в 1900 году призывавшая к оружию математиков на решение списка из двадцати трех труднейших математических проблем. Будучи юным отроком, избравшим путь математика, вы читаете этот список из двадцати трех проблем и слышите, как Гильберт говорит, что нет никаких ограничений тому, что математики могут открыт. Мы можем решить любую проблему, если достаточно умны и работаем над этим достаточно долго и упорно. Он предполагал, что нет никакого предел математическим достижениям.
Я думаю, это очень вдохновляло. Например, фон-Неймана. Когда он был молодым человеком, он предпринял попытку осуществить честолюбивый план Гильберта.
Поскольку Гильберт вряд ли мог заставить все это работать целиком, он фактически начинал с элементарной теории чисел, для начала с 1, 2, 3, 4, 5, … , даже не с действительных чисел, а с натуральных.
Но в 1931 году к великому и всеобщему удивлению (в том числе и фон-Неймана) Гедель показал, что это было невозможно, что это не могло быть сделано, по причине, о которой, я уверен, все знаете.
Гедель 1931
Это полностью противоречило тому, чего все ждали. Нейман сказал, что ему никогда в голову не приходило, что программа Гильберта не может быть выполнена. Фон-Нейман был крайне восхищен Геделем и помог ему получить положение в Институте Перспективных Исследований (Institute for Advanced Study).
Вот что следовало из того, что показал Гедель. Предположим, что вы имеете формальную аксиоматическую систему, имеющую дело с элементарной теорией чисел. С 1, 2, 3, 4, 5, сложением и умножением. И теперь предположим что такая система непротиворечива - это минимальное требование к ней (если вы действительно можете доказать в ней ложные утверждения, то это очень плохо!). Гедель показал, что еcли вы признаете, что система последовательна, то он может показать, что она неполна. Это был результат, полученный Геделем, и его доказательство очень остроумно использовало само-ссылку (само-референцию).
Гедель смог построить утверждение, относительно целых чисел, которое говорит о самом себе, что оно недоказуемо. Это был сокрушительный удар. Интеллектуальное воображение Геделя достойно восхищения! Ведь тогда каждый думал, что Гильберт прав.
Однако, я думаю, что подход Тьюринга все же был лучше.
Гедель 1931
Тьюринг 1936
Геделево доказательство 1931 года очень изобретательно, это действительно tour de force - проявление ловкости, силы ума и изобретательности. Должен признать, что когда я был юношей, пробовавшим понять все это, я мог читать это и следить за этим, шаг за шагом, но так или иначе я не мог никак почувствовать, что я улавливаю все это в целом. Но Тьюринг применил абсолютно иной подход.
Подход Тьюринга, и я думаю справедливо так говорить, является в некотором смысле более фундаментальным.
Фактически, Тьюринг делает больше чем Гедель. Тьюринг не только пришел к тому же заключению что и Гедель, но и показал, что не существует никакой разрешающей процедуры.
Смотрите. Если вы предполагаете, что у вас имеется формальная аксиоматическая система для арифметики, и она последовательна, то от Геделя вы знаете, что она не может быть полной. Но для нее все еще могла бы существовать разрешающая процедура. Все еще могла существовать некая механическая процедура, которая позволила бы вам решить является данное утверждение истинным или нет. Это все еще оставалось возможным после открытия Геделя. Но Тьюринг разрушил и это. Факт не существования разрешающей процедуры более фундаментален и тогда вы получаете неполноту как его следствие.
Как Тьюринг достиг этого? Я расскажу как он это сделал, потому что это трамплин для моей собственной работы. Способ, которым он это делал (и я уверен, вы слышали об этом) имеет отношение к тому, что называется Проблемой Остановки. Фактически, если вы обратитесь к работе Тьюринга 1936 года вы не найдете там слова "проблема остановки". Но суть этой проблемы, конечно же, там изложена.
Люди так же забывают, что Тьюринг говорил относительно "вычислимых чисел". Название этой его публикации: "On computable numbers, with an application to the Entscheidungsproblem" - "О вычислимых числах в приложении к проблеме разрешимости". Все помнят, что Проблема Остановки неразрешима и это следует из той самой работы, но не так много людей помнят, что Тьюринг там говорил относительно вычислимых действительных чисел. Моя работа так же имеет дело с вычислимыми и фатально невычислимыми действительными числами. Поэтому я хотел бы освежить в вашей памяти то, как выстроены аргументы Тьюринга.
Аргументы Тьюринга действительно уничтожают мечту Гильберта, и делается это простым способом. Метод Тьюринга основан только на диагональном процессе Кантора (для тех, кто знает, что это такое) приложенном к вычислению действительных чисел.
В том то и дело, что вся идея проста как дважды два, и она достаточно четко показывает, что мечта Гильберта, двух тысячелетняя кульминация развития того, что математики думали о математике, была неправильной. Работа Тьюринга - чрезвычайно глубока.
В чем суть аргументов Тьюринга?
Действительное число, как вы знаете, например 3.1415926..., является некой длинной, измеренной с произвольной точностью и имеет в своей записи бесконечное число цифр. И вычислимым вещественным числом, говорит Тьюринг, является такое число, для которого существует программа компьютера (или алгоритм) которая безостановочно вычисляет его цифры одну за другой. Например, имеется программа для числа pi и имеются алгоритм для решения алгебраических уравнений с коэффициентами в целых числах. На самом деле большинство действительных чисел, которые вы находите в анализе, вычислимы.
Однако они исключение, если вы знаете теорию множеств. Исключение, потому что мощность вычислимых действительных чисел счетное, в то время как мощность всех реальных чисел несчетно (вам не надо знать, что это означает). В этом суть идеи Тьюринга.
Идея состоит именно в этом. Вы составляете список из всех возможных компьютерных программ. Конечно, тогда еще не было никаких компьютерных программ, и Тьюринг был вынужден изобрести машину Тьюринга, которая оказалась огромным шагом вперед. Но теперь, зная, что такое программа, вы только говорите: представим себе воображаемый список, в котором занесена каждая возможная компьютерная программа.P1 [Гедель 1931]
P2 [Тьюринг 1936]
P3
P4
P5
P6
.
.
.
Если вы полагаете, что программы компьютера будут записаны в двоичном коде, то естественно думать о программе компьютера как о натуральном числе. Рядом с каждой компьютерной программой, первой, второй, третьей… вы выписывается натуральное число и само число, которое эта программа вычисляет, если она действительно вычисляет отдельные цифры некоторого действительного числа (чего может и не быть). Но если она бесконечно печатает цифры некоторого действительного числа, то мы выписываем их.
Возможно это 3.1415926....
Следом можно выписать другие, за ними - другие. P1 3.1415926... [Гедель 1931]
P2............. [Тьюринг 1936]
P3..........
P4.......
P5.....
P6...
.
.
.
И так вы составляете этот список. Возможно, некоторые из этих программ не печатают бесконечного числа цифр, потому что это программы, которые останавливаются или они содержат ошибку и в процессе выполнения они вылетают. И тогда на месте такой программы мы будем иметь незаполненный ряд в списке. P1 3.1415926...... [Гедель 1931]
P2................ [Тьюринг 1936]
P3................
P4................
P5
P6................
.
.
.
Эти проблем на самом деле не столь важна. И можно забыть относительно этой возможности. Поэтому вслед за Кантором, Тьюринг говорит, давайте спускаться по диагонали и смотреть на первую цифру первого числа, вторую цифру второго числа, третью цифру третьего . . . P1 -.d11_ d12 d13 d14 d15 d16 ... [Гедель 1931]
P2 -.d21 d22_ d23 d24 d25 d26 ... [Тьюринг 1936]
P3 -.d31 d32 d33_ d34 d35 d36 ...
P4 -.d41 d42 d43 d44_ d45 d46 ...
P5
P6 -.d61 d62 d63 d64 d65 d66_...
.
.
.
Прекрасно! Фактически, все эти цифры следуют за десятичной запятой. Так что первая цифра это первая цифра после десятичной запятой первого числа, вторая цифра - вторая цифра после десятичной запятой второго числа, третья - третьего числа, четвертая - четвертого, пятая - пятого. И это не важно, если пятая программа не производит пятую цифру. Это действительно не имеет значения. Поставьте на этом месте пробел и идите дальше.
Что вы делаете теперь? Вы изменяете эти цифры. Делаете их другими. Замените каждую цифру на диагонали и соберите эти измененные цифры в новое число с десятичной запятой впереди. Это будет новое действительное число.
То, что вы сейчас проделали - это и есть диагональный процесс (процедура) Кантора. В результате вы получили цифру, которая отличается от первой цифры первого числа, второй, второго, третьей, третьего, четвертой четвертого, пятой пятого… и вы собираете их в одно новое число. P1 -.d11_ d12 d13 d14 d15 d16 ... [Гедель 1931]
P2 -.d21 d22_ d23 d24 d25 d26 ... [Тьюринг 1936]
P3 -.d31 d32 d33_ d34 d35 d36 ...
P4 -.d41 d42 d43 d44_ d45 d46 ...
P5
P6 -.d61 d62 d63 d64 d65 d66_...
.
.
.
~d11 ~d22 ~d33 ~d44 ~d55 ~d66...
Это новое число не может стоять на каком-то месте в нашем списке из-за способа, которым оно было получено. Поэтому это невычислимое действительное число. Как Тьюринг переходит отсюда к Проблеме Остановки? Очень просто. Только спросите себе, а почему это число невычислимое? Я только что объяснил, как можно получить это число и это объяснение вполне могло бы служить алгоритмом получения данного числа. Чтобы вычислить N-ую цифру данного числа надо взять N-ую программу компьютера (вы можете это сделать), вы ее запускаете и ждете пока, она выдаст N-ную цифру и увидев ее, вы изменяете ее на другую. Что же нам здесь может помешать? Это все выглядит очень легким!
Проблема начинается в случае, если N-ная компьютерная программа никогда не выдаст N-ной цифры. А вы сидите и ждете у моря погоды. Это и есть Проблема Остановки, которую вы не можете решить: будет ли N-нная программа производить N-ную цифру вычисляемого ею числа или нет? Вот как Тьюринг получил неразрешимость Проблемы Остановки. Если бы вы могли решить Проблему Остановки, тогда бы вы могли бы выяснить поместит ли N-ная программа на N-нное место N-ную цифру. И если бы вы могли делать это, тогда бы вы фактически могли бы выполнять диагональную процедуру Кантора и вычислить действительное число, которое должно отличаться от любого реально вычислимого числа. Вычислить невычислимое число. Это и есть аргумент Тьюринга.
Почему это разрушило мечту Гильберта? Что Тьюринг доказал? То, что нет никакого алгоритма, никакой механической процедуры, которая решит, выдаст ли N-ую цифру N-ная компьютерная программа когда-либо или нет. Таким образом, не может иметься никакого алгоритма, который решит, останавливается программа компьютера когда-либо или нет (вопрос об N-ной цифры произведенной в соответствии с N-ной программой - частный случай).
Отлично. То что Гильберт хотел, было формальной аксиоматической системой, из которой должна была получена вся математическая истина, ничего кроме математическая истины и именно вся математическая истина. Если бы Гильберт мог достигнуть своей цели, то это автоматически дало бы нам механическую процедуру, чтобы решить будет ли программа компьютера когда-либо останавливаться или нет.
Почему?
Вы всего лишь пробегаете все возможные доказательства пока вы, или находите доказательство, что программа останавливается, либо вы находите доказательство, что программа никогда не остановиться. Так, если бы мечта Гильберта о конечном наборе аксиом (из которых должна следовать вся математическая истина) была бы возможна, тогда пробегая все возможные доказательства, вы могли бы проверить какое из них правильное, и вы бы тогда были способны решить остановиться ли любая программа компьютера или нет. В принципе могли бы. Но вы этого не можете согласно простым аргументам Тьюринга, который является всего лишь вариантом диагонального процесса Кантора, примененным к вычислению действительных чисел.
Это крайне просто!
Геделево доказательство изощренное и трудное. Аргументы же Тьюринга настолько фундаментальны, настолько глубоки, что все кажется естественным и неизбежным.
Но, конечно, они опирались на результат Геделя.
3. Вероятность остановки
и алгоритмическая хаотичность
Причина, по которой я так подробно рассказывал о Тьюринге и вычислимых действительных чисел, в том, что я собираюсь использовать эту процедуру для построения невычислимого действительного числа, намного более невычислимого, чем то, что строил Тьюринг.P1 -.d11_ d12 d13 d14 d15 d16 ... [Гедель 1931]
P2 -.d21 d22_ d23 d24 d25 d26 ... [Тьюринг 1936]
P3 -.d31 d32 d33_ d34 d35 d36 ...
P4 -.d41 d42 d43 d44_ d45 d46 ...
P5
P6 -.d61 d62 d63 d64 d65 d66_...
.
.
.
~d11 ~d22 ~d33 ~d44 ~d55 ~d66...
Здесь мы собираемся получить намного худший случай.
Как я могу получить намного более невычислимое действительное число? (И я должен буду показать насколько оно не вычислимо) Допустим не с помощью диагонального процесса Кантора.
Я получаю это число, которое я назвал  (омега) следующим образом: (омега) следующим образом:
 = = 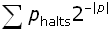
Это - всего лишь вероятность остановки. Это разновидность математического каламбура. Фундаментальный результат Тьюринга в том, что Проблема Остановки является неразрешимой. Не существует никакого алгоритма, который разрешит Проблему Остановки. Мой же фундаментальный результат в том, что Вероятность Остановки является алгоритмически не представимой (не редуцируемой) или алгоритмически случайной.
Чем в точности является вероятность остановки? Я записал это таким выражением:
 = = 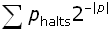
Вместо того, чтобы смотреть на отдельные программы и выяснять остановиться ли она или нет, вы сваливаете все программы вместе в один мешок. Если вы пишете программу компьютера наугад, подбрасывая монету, для выбора каждого нового бита, что окажется вероятностью того, что такая программа остановиться? Вы думаете, о программах как о цепочках битов и вы производите каждый бит независимой монетой. Так, если программа длинной в N бит, то вероятность того, что вы получите некоторую специфическую программу 2-N . Любая программа P, которая останавливается, вносит вклад 2-|p| два в степени минус ее размер в битах, число бит в ней к вероятности ее остановки.
Между прочим, имеется техническая деталь, которая очень важна и не работала в ранней версии алгоритмической теории информации. Вы не могли писать так:
 = = 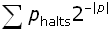
Это дало бы бесконечность. Техническая деталь в том, что никакое расширение (продление) действующей программы не является работающей программой. Только в этом случае сумма
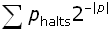
оказывается между нулем и единицей. В противном случае она оказалась бы бесконечностью. Мне потребовалось десяток лет, чтобы получить это заключение. Оригинальная версия алгоритмической теории информации 1960-х годов неверна. Одной из причин, почему она оказалась неверной, в том, что вы даже не можете определить это число
 = = 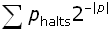
Я думаю, нужно кое что пояснить. phalts - это вероятность остановки конкретной программы P. Если она останавливается, значит phalts=1, если нет phalts=0 .То есть этот множитель как бы отбирает для суммирования только те программы, которые останавливаются. Обозначение |p| - это длинны (в битах) данной программы P. То есть N Прим. А.С.
В 1974 году я переделал алгоритмическую теорию информации для "само-ограничивающихся" программ, и затем нахожу вероятность остановки  (омега) (омега)
И так, мы получаем, что число  - вероятность, значение которой где-то между нулем и единицей. - вероятность, значение которой где-то между нулем и единицей.
0 <  = = 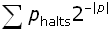 < 1 < 1
так же, как и любая другая вероятность.
Главная идея - вы получаете каждый бит программы подбрасыванием монеты и спрашиваете, какова вероятность, что она остановиться? Это число, вероятность остановки  , не просто невычислимое действительное число. , не просто невычислимое действительное число.
Тьюринг уже знал, как такое число получить. Невычислимое в некоторых разрядах. Но  невычислима самым худшим образом. Позвольте мне показать некоторые ключевые моменты и продемонстрировать, насколько оно невычислимое. невычислима самым худшим образом. Позвольте мне показать некоторые ключевые моменты и продемонстрировать, насколько оно невычислимое.
Суть этого - алгоритмическая не сжимаемость. Если вы хотите получить первые N бит числа  с помощью компьютерной программы, если вы хотите иметь компьютерную программу которая будет печатать первые N бит числа с помощью компьютерной программы, если вы хотите иметь компьютерную программу которая будет печатать первые N бит числа  , и затем она должна остановиться, то эта программа должна быть длинной не менее N бит. По существу вы только распечатаете (выводите) константы, которые находятся в программе так как вы не можете сжать, упаковать первые N бит , и затем она должна остановиться, то эта программа должна быть длинной не менее N бит. По существу вы только распечатаете (выводите) константы, которые находятся в программе так как вы не можете сжать, упаковать первые N бит  . .
 является действительным числом, и вы могли бы записать его в двоичном коде. И если вы хотите получить первые N бит с помощью компьютерной программы, то по существу вам остается только поместить все эти биты как константу. Это алгоритмически несжимаемая, нередуцируемая, не упаковываемая информация. Не существует никакого более краткого ее описания. является действительным числом, и вы могли бы записать его в двоичном коде. И если вы хотите получить первые N бит с помощью компьютерной программы, то по существу вам остается только поместить все эти биты как константу. Это алгоритмически несжимаемая, нередуцируемая, не упаковываемая информация. Не существует никакого более краткого ее описания.
Теперь абстрактная суть этого предмета. Позвольте показать больше конкретных примеров того, насколько случайно  . Эмиль Борель (Emile Borel) на рубеже этого столетия был одним из основателей теории вероятностей. . Эмиль Борель (Emile Borel) на рубеже этого столетия был одним из основателей теории вероятностей.
Эмиль Борель…
И так, мы остановились на Эмиле Бореле, и он говорил о вещах, которые он назвал нормированными числами.
Эмиль Борель - нормированное число.
Что такое нормированное действительное число? Люди вычислили pi до миллиардной цифры после запятой, возможно до двух миллиардной цифры. Оной из причин для этого, помимо простого спортивного интереса и установления мирового рекорда, являлся вопрос о том, появляется ли каждая цифра одинаковое число раз?
Похоже, что каждая из цифры от 0 до 9 встречается в 10% случаев десятичного разложения числа pi. Это похоже на правду, если взглянуть на полученный результат, но никто не может этого доказать. Я думаю, что подобный вопрос вполне уместен и для квадратного корня из 2, хотя это не настолько популярное число, что бы спрашивать о нем.
Теперь позвольте мне описать некоторые результаты Бореля, сделанные на рубеже столетия, когда он был пионером современной теории вероятности. Выберете действительное число в интервале от 0 до 1. Это действительное число с запятой впереди, без целой части. Если вы выбираете целое число в интервале от нуля до единицы, Борель показал, что с вероятностью 1 оно будет "нормированным". Нормированным, это значит, что когда вы пишите десятичное разложение числа, то каждая цифра встретиться в нем ровно в 10% случаев и так будет при любом другом основании счисления. Например, в двоичной системе 0 или 1 будут встречаться ровно в 50% случаев. Подобное происходит и с блоками цифр. Это называется абсолютно нормированным вещественным числом Бореля и он показал, что с вероятностью один, если вы наугад выбираете число в интервале между 0 и 1 оно имеет это свойство. Только возникает одна проблема. Он не знал, является ли pi нормированным, он не знал, является ли корень из 2 нормированным. Фактически он не мог показать ни одного отдельного, конкретного примера нормированного числа.
Первый пример нормированного действительного числа был обнаружен кембриджским другом Алана Тьюринга по имени Давид Чамперноун (David Champernowne), который до сих пор еще жив и сейчас является известным экономистом. Тьюринг был в восторге от него и, я думаю, он называл его "Чемпион" (Champ) потому что Чамперноун выполнил и опубликовал эту работу как новатор. Это число известно как число Чамперноуна. Позвольте продемонстрировать вам его:
.01234567891011121314 ... 99100101 ...
дальне все продолжается в том же духе. Вы ставите десятичную запятую, потом вы пишете 0 1 2 3 4 5 6 7 8 9 потом 10 11 12 13 14 до 99, тогда 100 101.
Вы продолжаете этим забавным образом дальше. Это число и называется числом Чамперноуна и Чамперноун показал, что оно нормально по основанию 10. Никто не знает, является ли оно нормальным в других базах, я думаю, этот вопрос все еще долго будет открыт. Но в десятичном основании каждая цифра от 0 до 9 в пределе встречаются с частотой 10%, каждый возможный блок из пары цифр, в пределе встречается с частотой ровно 1%, и так далее. Это и называется быть нормированным по основанию десять. Но никто не знает, что случиться при другом основании.
Причина, по которой я говорю обо всем этом в том, что исходя из факта, что вероятность остановки является алгоритмически не редуцируемой информацией следует что  является нормированным в любом основании. Это легко доказать пользуясь идеей относительно кодирования и сжатия информации, которые возвращаются еще к Шеннону (Shannon). Здесь мы имеем пример абсолютно нормального числа. Я не знаю, что на самом деле вы думаете об этом, но это обыкновенное действительное число, которое вполне отвечает всем требованиям, предъявляемым к подобным числам, которое Борель мог бы вполне признать. Число Чамперноуна совсем не обладает таким свойством! является нормированным в любом основании. Это легко доказать пользуясь идеей относительно кодирования и сжатия информации, которые возвращаются еще к Шеннону (Shannon). Здесь мы имеем пример абсолютно нормального числа. Я не знаю, что на самом деле вы думаете об этом, но это обыкновенное действительное число, которое вполне отвечает всем требованиям, предъявляемым к подобным числам, которое Борель мог бы вполне признать. Число Чамперноуна совсем не обладает таким свойством!
Число  случайно в гораздо большем смысле. Я бы выразил это таким образом. Его невозможно отличить от результата, полученного подбрасыванием справедливой монеты. Фактически это число показывает, что вы имеете полный хаос и непредсказуемость, имеете отсутствие структуры в чистой математике! Таким же образом, как Тьюрингу понадобился всего лишь диагональный процесс, что бы уничтожить мечту Гильберта, вам нужно только записать это выражение случайно в гораздо большем смысле. Я бы выразил это таким образом. Его невозможно отличить от результата, полученного подбрасыванием справедливой монеты. Фактически это число показывает, что вы имеете полный хаос и непредсказуемость, имеете отсутствие структуры в чистой математике! Таким же образом, как Тьюрингу понадобился всего лишь диагональный процесс, что бы уничтожить мечту Гильберта, вам нужно только записать это выражение
 = = 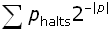
И это показывает, что имеется область чистой математики, где рассуждения полностью бесполезно, где вы натыкаетесь на непроницаемую стеру. Это все что вам требуется. Только это -  - вероятность остановки. - вероятность остановки.
Почему я говорю об этом? Допустим, вы хотите использовать аксиомы, что бы доказать кое что о некоторых битах этого числа  . Я уже сказал вам, что это не вычислимо, так? Оно не вычислимо подобно числу, которое Тьюринг строил, используя диагональный метод Кантора. Поэтому мы знаем, что нет никакого алгоритма, который бы вычислял цифру за цифрой или бит за битом числа . Я уже сказал вам, что это не вычислимо, так? Оно не вычислимо подобно числу, которое Тьюринг строил, используя диагональный метод Кантора. Поэтому мы знаем, что нет никакого алгоритма, который бы вычислял цифру за цифрой или бит за битом числа  . Но давайте попробуем доказать то, что отдельные биты в нем опираются на формальную аксиоматическую систему. Что произойдет? . Но давайте попробуем доказать то, что отдельные биты в нем опираются на формальную аксиоматическую систему. Что произойдет?
Ситуация крайне плохая. Это похоже на следующее.
Предположим, что вы имеете формальную аксиоматическую систему, которая состоит из N бит формальной аксиоматической системы (позже я объясню, что это означает "биты формальной системы"). Получается что из формальной аксиоматической системы размерностью N, то есть размером в N бит, вы можете доказать то, что имеется некоторое значение у некоторых бит в некотором разряде. У некоторых N бит числа  . .
Теперь что я подразумеваю под формальной аксиоматической системой размером в N бит?
Вы помните, что сущность формальной аксиоматической системы - механическая процедура для проверки следует ли формальное доказательство из правил или нет. Это - программа компьютера. Конечно, во времена Гильберта не имелось никаких программ и компьютеров, но после Тьюринга, после изобретения им его машины, вы теперь можете точно определить что такое программа и мы теперь очень хорошо знакомы с подобными математическими объектами.
Проверяющий доказательства алгоритм, есть сущность любой формальной аксиоматической системы в смысле Гильберта - это программа компьютера и надо только посмотреть из скольких бит состоит эта программа.* Это по существу означает вопрос: сколько бит надо взять чтобы описать правила игры: ее аксиомы и правила вывода. Если это N бит, то вы способны уверенно сказать что первый бит  в двоичном исчислении 0, второй 1, третий бит 0 затем имелся бы промежуток (пробел) после которой вы были бы способны доказать что тысячный бит 1. Но в состоянии разъяснить только N случаев, если ваша формальна система состоит из N бит. в двоичном исчислении 0, второй 1, третий бит 0 затем имелся бы промежуток (пробел) после которой вы были бы способны доказать что тысячный бит 1. Но в состоянии разъяснить только N случаев, если ваша формальна система состоит из N бит.
Позвольте мне объяснить детальнее, что это означает. Это означает, что вы можете получить на выходе столько, сколько поместили на входе. Если вы хотите доказать, что некоторый отдельный бит двоичного разложения числа  , в некотором его месте, является 1 или 0, то существует только единственный способ это сделать - взять это как гипотезу, как постулат, как аксиому. Потому что это не редуцируемая математическая информация. Это ключевая фраза, которая в действительности содержит всю идею. , в некотором его месте, является 1 или 0, то существует только единственный способ это сделать - взять это как гипотезу, как постулат, как аксиому. Потому что это не редуцируемая математическая информация. Это ключевая фраза, которая в действительности содержит всю идею.
Irreducible Mathematical Information
И так, чего мы добились?
Мы имеем довольно простой математический объект, который полностью непостижим нами. Биты  (омеги) не имеют никакой структуры. В их расположении нет никакой схемы, никакой закономерности, которую мы, как математики, могли бы постичь. Если вас интересует вывод о том, каким будет отдельный бит в той или иной части этого числа, являются ли он 0-лем или 1-цей, то рассуждения об этом полностью бесполезны. Математические рассуждения здесь несостоятельны и бессильны. Как я уже говорил, единственный путь, которым можно построить здесь формальную аксиоматическую систему, это поместить биты как предположения, гипотезы, что означает, что вы не используете никаких рассуждений, логических выводов. В конце концов, что-либо можно узаконить, если взять это как аксиому, которую вы добавляете к множеству своих аксиом. И это все что вы можете здесь сделать, так как это - самый худший случай из всех возможных. Это математически не редуцируемая информация. Это тот случай, где нет никакой корреляции, никакой структуры, никакой формы, которую бы мы могли когда-нибудь уловить и почувствовать. (омеги) не имеют никакой структуры. В их расположении нет никакой схемы, никакой закономерности, которую мы, как математики, могли бы постичь. Если вас интересует вывод о том, каким будет отдельный бит в той или иной части этого числа, являются ли он 0-лем или 1-цей, то рассуждения об этом полностью бесполезны. Математические рассуждения здесь несостоятельны и бессильны. Как я уже говорил, единственный путь, которым можно построить здесь формальную аксиоматическую систему, это поместить биты как предположения, гипотезы, что означает, что вы не используете никаких рассуждений, логических выводов. В конце концов, что-либо можно узаконить, если взять это как аксиому, которую вы добавляете к множеству своих аксиом. И это все что вы можете здесь сделать, так как это - самый худший случай из всех возможных. Это математически не редуцируемая информация. Это тот случай, где нет никакой корреляции, никакой структуры, никакой формы, которую бы мы могли когда-нибудь уловить и почувствовать.
4. Хаотичность в арифметике
Хорошо, но какое отношение это имеет к хаотичности в арифметике? Теперь мы вернемся к Геделю (я прошелся по нему довольно поверхностно), давайте теперь вернемся к нему.
Тьюринг говорит, что вы не можете использовать доказательство, чтобы решить остановиться ли программа или нет. Вы не можете для любой программы доказать, что она остановится или не остановиться. Это то - как он уничтожил мечту Гильберта о универсальной математике. Я получаю для нас еще большую неприятность, рассматривая другого рода вопрос, а именно, можете ли вы доказать что пятый бит этого специфического вещественного числа:
 = = 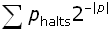
является 0 или 1? Или выяснить является ли восьмой бит 0 или 1? Но это - странно выглядящий вопрос. Кто что-либо слышал о Проблеме Остановки в 1936 году? Это не тот тип вопроса, который обычно волнует математиков. Конечно, мы имеем неприятности, но в вопросах довольно далеких от обычной математики.
Даже если вы не можете иметь формальную систему, которая доказывала бы остановиться программа или нет, она, эта система, могла бы быть хороша для всего остального, и тогда вы могли бы иметь слегка измененную версию мечты Гильберта. То же самое могло иметь место и с вероятностью остановки  . Если Проблема Остановки выглядит немного причудливой (а так и было в 1936 году) то "тип . Если Проблема Остановки выглядит немного причудливой (а так и было в 1936 году) то "тип  " - объект еще более искусственный и, конечно, выглядит оно причудливо. Кто когда-либо слышал о вероятности остановки? Это не тот типа объектов, которым обычно математики занимаются. Поэтому все эти заботы по поводу всех этих выводов о неполноте - только моя забота. " - объект еще более искусственный и, конечно, выглядит оно причудливо. Кто когда-либо слышал о вероятности остановки? Это не тот типа объектов, которым обычно математики занимаются. Поэтому все эти заботы по поводу всех этих выводов о неполноте - только моя забота.
Гедель уже стоял перед этой проблемой со своим утверждением, которое является истинным, но недоказуемым. Это утверждение, которое говорит о себе, что оно недоказуемо. Это тот вид объекта, который никогда не встречается в реальной математике. Одним из ключевых моментов доказательства Геделя в том, что он сумел построить арифметическое утверждение, которое говорит о себе, что оно недоказуемо. Он получил само-ссылающееся утверждение в терминах элементарной теории чисел, для чего потребовалось очень много ума.
Имеется много работ, построенных на Геделевой работе, показывающих, что проблемы связанные с вычислениями, эквивалентны арифметическим проблемам, связанным с целыми числами. Множество примеров приходит в голову. Джулия Робинсон (Julia Robinson), Хилари Путнэм (Hilary Putnam) и Мартин Дэвис (Martin Davis) выполнили часть важной работы и, в конце концов, ключевой результат был получен в 1970 году Юрием Матисевичем.
Он построил диофантово уравнение, которое является алгебраическим уравнением, использующим только целые числа с большим количеством переменных. Одна из переменных - К, используется как параметр. Это полиномиальное уравнение с целыми коэффициентами, и все неизвестные так же должны быть целыми. Таковы диафантовы уравнения. Я сказал, что одно из неизвестных -параметр. Уравнение Матисевича имеет решение при специфическом параметре К, если и только если К-ая программа компьютера останавливается.
В 1900 году Гильберт предложил найти алгоритм, который решит, является ли диофантово уравнение, алгебраическое уравнение использующее только целые числа, разрешимым или нет. Это так называемая десятая проблема Гильберта.
Это была десятой в его известном списке из двадцати трех проблем. Что показал Матисевич в 1970 году, что эта проблема является эквивалентной проблеме о том, останавливается ли произвольная программа компьютера или нет. Так что Проблема Остановки Тьюринга - настолько же трудна, как и десятая проблема Гильберта. Выяснить остановиться ли произвольная программа компьютера или нет, настолько же трудно, как и выяснить имеет ли произвольное алгебраическое уравнение решение в целых числах. Для этого нет никакого алгоритма, поэтому десятой проблемы Гильберта не может быть решена, к чему и пришел в результате Матисевич в 1970-м году.
Матисевича увлекла работа в этой области. Например, есть работа, которую он выполнил в сотрудничестве с Джеймсом Донес (James Jones) в 1984 году. Я использовал ее, следуя по стопам Геделя, и его примеру. Вы видите, как я показал, что в битах числа О наблюдается абсолютная хаотичность, отсутствие какой-либо формы, полная бесструктурность. Рассуждения являются полностью бесполезными, если вы заинтересуетесь отдельными битами этого числа.
Следуя Геделю, давайте преобразуем это в кое-что из элементарной теории чисел, так как если вы можете с этим столкнуться в элементарной теории чисел - это фундаментальная проблема. Элементарная теория чисел 1, 2, 3, 4, 5, сложения и умножения, которая восходит еще к древним грекам, является наиболее твердой частью всей математики. В теории множеств вы имеете дело со странными объектами, типа кардинала, но здесь вы не имеете дела даже с производными и интегралами. Здесь вы имеете дело только с целыми числами. И опираясь на результаты Джеймсом Донеса и Матисевича я действительно могу получить омегу  арифметически и получить хаотичность в элементарной теории чисел.** арифметически и получить хаотичность в элементарной теории чисел.**
Что я получаю - это показательная функция диофантового уравнения с параметром. "Показательная функция диофантового уравнения с параметром" означает, что здесь допускаются переменные в степенях. В отличии от этого, Матисевич, показывая что десятая проблема Гильберта неразрешима, использовал только многочлен диофантового уравнения, а значит, показатели степени у него всегда Y - натуральная константа. Я позволяю X. Но остается неизвестным, могу ли я это делать? Могло случиться так, что я все же могу справиться с многочленом диофантового уравнения. Это открытый вопрос - который, я полагаю, не решен окончательно.
Но пока вся что я имею - показательная диофатнова функция с семнадцатью тысячами переменных. Это уравнение занимает две сотни страниц текста и имеет одну переменную - параметр.
Это уравнение, где каждая постоянная - целое число, натуральное число, и все переменные так же натуральные числа, то есть положительные целые числа (на самом деле неотрицательные целые числа). Одна из переменных - это параметр, и вы изменяете значение этого параметра, подставляя числа 1, 2, 3, 4, 5. Тогда вы спрашивает: уравнение имеет конечное или бесконечное число решений? Мое уравнение построено так, чтобы оно имело конечное число решений, если специфический, отдельный бит омеги  является "0", и имеет бесконечное число решений, если этот бит - "1". Так вывод о том, имеет ли моя показательная функция диофантового уравнения в каждом отдельном случае конечное или бесконечное число решений зависит от определения конкретного бита омеги является "0", и имеет бесконечное число решений, если этот бит - "1". Так вывод о том, имеет ли моя показательная функция диофантового уравнения в каждом отдельном случае конечное или бесконечное число решений зависит от определения конкретного бита омеги  - вероятности остановки. Это абсолютно невозможно, потому что - вероятности остановки. Это абсолютно невозможно, потому что  - не редуцируемая математическая информация. - не редуцируемая математическая информация.
Позвольте мне подчеркнуть различие между этой конструкцией, и работай Матисевича по решению десятой проблемы Гильберта. Матисевич показал, что имеется многочлен диофантова уравнения со следующим свойством: вы изменяете параметр, и спрашиваете уравнение, имеет решение?
И это оказывается эквивалентно Проблеме Остановки Тьюринга и поэтому не подвластно математическим рассуждениям.
Чем это отличается от того, что сделал я? Я использую показательную функцию диофантово уравнения, что означает, что я позволяю переменным быть и в показателе степени. Матисевич позволяет только постоянные показатели степени. Большая разница - Гильберт просил об алгоритме, показывающем имеет ли решение диофантово уравнение или нет. Мой вопрос в том, как получить хаотичность в элементарной теории чисел в арифметике натуральных чисел, является несколько более сложным. Вместо выяснения того, имеется ли решение, я спрашиваю, имеется ли конечное или бесконечное число решений - более абстрактный вопрос. Это различие необходимо понимать.
Мое двухсот страничное уравнение построено так, что бы иметь конечное или бесконечное число решений в зависимости от того, является ли специфический бит вероятности остановки 0-ем или 1-ей. По мере того, как вы изменяете параметр, вы получаете каждый отдельный бит числа  . Уравнение Матисевича построено так, что бы оно имело решение, если и только если некоторая программа когда-либо остановиться. Поскольку вы изменяете параметр, вы получаете каждую отдельную программу компьютера. . Уравнение Матисевича построено так, что бы оно имело решение, если и только если некоторая программа когда-либо остановиться. Поскольку вы изменяете параметр, вы получаете каждую отдельную программу компьютера.
Таким образом даже в арифметике вы находите абсолютное  -бесструктурность, -бесструктурность,  - хаотичность и не редуцируемую математическую информацию. Рассуждения полностью бессильны в таких областях арифметики. Мое уравнение показывает, что это так. Я сказал раньше, что прежде чем получить это уравнение, я использовал идеи оригинальной Геделевой работы 1931-го года. Но это была работа Джонса и Матисевича 1984 года, которая, в конце концов, дала мне инструмент, в котором я нуждался. - хаотичность и не редуцируемую математическую информацию. Рассуждения полностью бессильны в таких областях арифметики. Мое уравнение показывает, что это так. Я сказал раньше, что прежде чем получить это уравнение, я использовал идеи оригинальной Геделевой работы 1931-го года. Но это была работа Джонса и Матисевича 1984 года, которая, в конце концов, дала мне инструмент, в котором я нуждался.
И так я утверждаю, что имеется хаотичность в элементарной теории чисел, в арифметике натуральных чисел. Это непроницаемая каменная стена. Это самый плохой случай. От Геделя мы знаем, что мы не можем заставить формальную аксиоматическую систему быть полной. Мы знаем, что столкнулись с неприятностью, и Тьюринг показал нам, насколько фундаментальна эта неприятность, но я показываю крайний случай, когда формальный вывод терпят полную неудачу.
Я не буду вдаваться в детали, но позвольте мне выразиться в неопределенных информационно-теоретических терминах. Уравнение Матисевича дает вам N вопросов с ответами типа да/нет, которые собираются только в Log2N бит алгоритмической информации. Мое уравнение дает вам N арифметических вопросов, с ответами типа да/нет, которые являются непреодолимой, нередуцируемой математической информацией.
5. Экспериментальная математика
Позвольте мне немного сказать, буквально минуту, о там что, я отстаивал всеми средствами. Прежде всего, связь с физикой. Имелось большие трудности, в начале развития квантовой механики, потому что квантовая теория недетерминирована. Эйнштейн именно за это ее не любил. Он сказал "бог не играет в кости!" Но поскольку, я уверен, все знают о хаосе в нелинейной термодинамике, мы теперь поняли, что даже в классической физике мы получаем хаотичность и непредсказуемость. Моя работа выполнена в том же духе. Это показывает что чистая математика, фактически элементарная теория целых чисел, арифметика целых чисел 1,2,3,4,5, находятся в том же самом состоянии. Мы получаем хаотичность там тоже! Как бы выразились газетчики, бог не только играет в кости в квантовой механике и классической физике, но даже в чистой математике, даже в элементарной теории чисел! Поэтому если новая парадигма и появится, то хаотичность будет лежать в ее основе. Между прочим, хаотичность так же лежит в основе квантовой теории поля как виртуальные частицы действия и интегралы пути Фейнмана (суммы по всем уровням) демонстрируют это очень ясно. Так что моя работа перекликается с большим количеством работ в физике, что объясняет, почему меня часто приглашают на встречи физиков.
Однако самый важный вопрос не физика, а математика. Я слышал, что Гедель однажды написал письмо своей матери, которая осталась в Европе. Вы знаете, Гедель и Эйнштейн были друзьями в Институте Перспективного Развития (Institute for Advanced Study). Их часто видели идущими по улице вместе.
Очевидно, Гедель действительно написал письмо своей матери, где он говорил, что работа Эйнштейна имела на физиков и на то, как они делают физику большое влияние, и он был разочарован от того, что его работа не имела того же самого эффекта на математиков. Она действительно никак не повлияло на то, как математики продолжают делать свою обычную работу. Поэтому я думаю это ключевой вопрос: Как вы действительно должны делать математику?
Я претендую на то, что имею намного более сильный результат неполноты. Если такое возможно, то становится ясным: должна ли математика двигаться обычным путем или нет. Как обычно делается математика? Несмотря на то, что каждый знает, что любой конечный набор аксиом неполон, как математики фактически работают? Давайте предположим, что вы имеете догадку над которой работаете в течении нескольких недель и вы верите в это, потому что вы проверили большое количество случаев на компьютере. Возможно ваша догадка касается простых чисел и в течении двух недель вы пробовали доказать это. В конце двух недель вы говорите: хорошо, возможно причина, по которой я не могу доказать это - Геделева теорема о неполноте?! Поэтому давайте добавим эту истину как новую аксиому! Если вы воспринимаете теорему Геделя серьезно, вы можете использовать этот прием чтобы продвигаться дальше. Математики будут смеяться, но физики, фактически, именно таким образом и продвигаются.
Посмотрите на историю физики. Начните с Ньютона. Вы не можете вывести уравнения Максвелла из ньютоновской механики. Это новая область - возникшая из опыта - и поэтому вы нуждаетесь в новых аксиомах, чтобы описать все это.
Посмотрим на специальную теорию относительности.... Ну, в общем, она почти присутствует в уравнения Максвелла. Но уравнение Шредингера не выводятся из физики Ньютона и уравнений Максвелла. Это новый опыт и вы нуждаетесь в новых аксиомах. Поэтому физики привыкли к идее, что когда вы начинаете экспериментировать в меньшем масштабе или с новыми явлениями, то вы можете нуждаться в новых принципах, дабы понять и объяснять то, что происходит.
Математики, не смотря на неполноту, не ведут себя подобно физикам. На подсознательном уровне они все еще предполагают, что небольшой набор принципов является достаточным. В глубине души они предполагают, что если вы не можете доказать результат, то это ваша собственная ошибка. Это, конечно хороший подход, брать вину на себя прежде, чем винить кого-то еще, но давайте посмотрим на вопрос типа гипотезе Римана. Физики говорили бы, что имеется вполне достаточно экспериментальных доказательств, подтверждающих гипотезу Римана, и следовало бы двигались дальше, взяв эту гипотезу как рабочую.
Что такое гипотеза Римана? Имеется много гипотез связанных с распределением простых чисел, которые могут быть разрешены, если принять гипотезу Римана. Используя компьютер, люди проверяют эти догадки, и они работают красиво. Это четкие, аккуратные формулы, но никто не может их доказать. Многие из них следуют из гипотезы Римана. Коль гипотеза полезно, Коль она объясняет многие данные, то для физика этого было бы вполне достаточно. Конечно, физик должен быть всегда готов, чтобы сказать: "Ох, ох! Я опростоволосился!" Потому что эксперимент может впоследствии противоречить теории. Это случается очень часто.
В физике элементарных частиц вы постоянно выдвигаете теории, и постоянно большая часть из них быстро умирает. Но математикам не нравится необходимость быть готовым идти на попятные. Но если вы всегда играете в защите, то ваша проблема в том, что вы можете только потерпеть неудачу, но не выиграть и я полагаю, что так и будет.
Я думаю, всем очевидно к чему я веду. Я полагаю, что элементарная теория чисел и остальная часть математики должны развиваться больше в духе экспериментальной науки, и там должны быть приняты новые принципы. Я считаю, что утверждение Эвклида, что аксиомы -самоочевидная истина - большая ошибка. Уравнения Шреденгера, конечно же, не самоочевидная истина! И гипотеза Римана также не самоочевидна, но все это очень полезно.
Мы, математики, не должны игнорировать неполноту. Работая только наверняка, мы терпим неудачу в тех случаях, в которых могли бы добиться результата. Происходит то, как будто бы физики сказали: хорошо, никаких уравнений Шреденгера, никакого Максвелла, мы останавливаемся на Ньютоне, все должно быть выведено только из законов Ньютона. (Максвелла даже пробовал это сделать. Он строил механическую модель электромагнитного поля. К счастью ее не преподают в колледжах.)
Я предложил все это двадцать лет назад, когда я начал получат эти результаты - теоретические результаты неполноты. Независимо появилась новая школа в философии математики -"квазиэмпирическая" школа мысли относительно основ математики. Существует книга Тимозко (Tymoczko), "Новое направление в философии математики " ("New Directions in the Philosophy of Mathematics"). Это прекрасное собрание статей. Другая работа: "Поиск уверености" Джона Кести ("Searching for Certainty" John Casti), которая содержит прекрасную главу посвященную математике. Последняя часть главы говорит о квазиэмпирическом подходе.
Между прочим, Лакатос (Lakatos), который был сторонником этого движения, был в Кембридже в то время. Тогда он покинул Венгрию.
Главные школы математической философии в начале этого столетия были школа Рассел и Уайтхеда (Russell, Whitehead) проповедовавших взгляды, что логика есть основа для всего, школой формалиста Гильберта и "интуиционистская" конструктивистская школа Брауэра. Некоторые люди думают, что Гильберт полагал, что математика бессмысленная игра с символами на бумаге. Но нет! Он так сказал, чтобы быть абсолютно четким и ясным. Он так сказал для того, чтобы математика была понята всеми одинаково. Для этого мы должны четко определить четкие правила для выяснения правильности доказательства настолько точно, что те стали механическими. Тот, кто думал, что математика бессмыслен, не мог быть настолько энергичен, сделать в ней так много, и быть в ней таким вдохновителем идей.
С самого начала большинство математиков поддержали Гильберта. Даже после Геделя и даже после более решительного Тьюринг, показавшего, что мечта Гильберта не работает, математическая практика продолжалась в духе Гильберта. Конструктивистский подход Брауэра, главным образом, рассматривался как помеха. Что касается Рассела и Уайтхеда, то они имели много проблем, выводя всю математику из логики. Если вы выводите всю математику из теории множеств, то вы обнаруживаете, что целые числа очень хорошо определяются в терминах множеств (фон-Нейман работал над этим). Но тогда выясняется, что они имеют все те проблемы, которые возникают с множествами. Вы не делаете натуральные числа более устойчивыми, выстраивая их на чем-то зыбком.
Но теперь все пошло вверх дном. Все пошло вверх дном не из-за какого-то философского спора, не из-за результатов Геделя или результатов Тьюринга или моих результатов неполноты. Это пошло вверх дном по очень простой причине -компьютеры!
Компьютеры, как вы все знаете, изменили способ, которым мы все делаем. Компьютер чрезвычайно и значительно увеличил наш математический опыт. На них легко делать вычисления, проверять многие случаи, управлять вычислительными экспериментами. Компьютер так значительно увеличил математический опыт, что для того чтобы справиться с чем-то, люди вынуждены пользоваться более прагматическим, прикладными методами. Прагматичные математики переходят к экспериментальным наблюдениям. Эта новая тенденция часто называется "экспериментальная математика". Это название подойдет ко многому, что делается в области хаоса, фракталов и нелинейной динамики.
Часто так происходит, что когда вы ставите вычислительный эксперимент на компьютере, вычислительные эксперименты с уравнениями, вы обнаруживаете кое-какие закономерности и в результате догадываетесь, в чем дело. Конечно, здорово если вы можете это доказать. Особенно, если доказательство короткое. Я не уверен, что доказательства в тысячу страниц очень сильно помогает что-то понять. Но если это короткое доказательство, то это лучше чем отсутствие доказательства. А если вы имеете несколько доказательств с различных точек зрения, то это совсем хорошо!
Но иногда вы не можете найти доказательство и вы не можете ждать чего-то еще, что бы найти доказательство и вы должны продолжать в том же духе. Поэтому математики иногда продолжают рабочие гипотезы на основе результатов компьютерных экспериментов. Конечно, если это физик, ставящий эксперимент на компьютере, тогда это конечно хорошо. Он всегда всецело доверяет эксперименту. Но теперь и целочисленные математики порой работают в такой манере. Имеется новый журнал, который называется "Журнал Экспериментальной Математики" (Journal of Experimental Mathematics). Они должны были бы поместить меня в свою редколлегию, так как я предлагал это в течение двадцати лет, основываясь на своих информационно-теоретических идеях.
И так, окончательно, это не Гедель, не Тьюринг и не мои результаты заставляют математиков поворачиваться в сторону экспериментального направления исследования математики. В квази-эмпирическом направлении. Причина того, что математики изменяют своей рабочей привычки - компьютер! Я думаю, что это превосходная вещь! (Забавно и то, что из трех философских школ, логицизма, формализма и конструктивизма наиболее пренебрежителен к ним был Брауэр, кто имел конструктивистский подход за многие годы до того, как компьютер дал сильнейший толчок развитию конструктивизму.)
Конечно, факт того, что все начали что-то делать, не означает, что так и должно быть. Конечно, изменения наблюдаются не из за Геделевой теоремы. не из за теоремы Тьюринга, или моей теоремы, а из-за компьютера. Но я думаю, что серия работ, которые я выполнил, обеспечивает некоторое теоретическое обоснование тем кто, так или иначе, делают работу в математике, не сильно беспокоясь о теоретическом обосновании. И я думаю, что вопрос о том, как мы должны делать математику на самом деле, требует, по крайней мере, другой серии работ. На этом в основном и все, что я и хотел вам сказать.
Спасибо вам за внимание!
Библиография
[1] G. J. chaitin, Algorithmic Information Theory, revised third printing, Cambridge University Press, 1990.
[2] G. J. chaitin, Information, Randomness & Incompleteness, second edition, World Scientific, 1990.
[3] G. J. chaitin, Information-Theoretic Incompleteness, World Scientific, 1992.
[4] G. J. chaitin, "Exhibiting randomness in arithmetic using Mathematica and C," IBM Research Report RC-18946, 94 pp., June 1993. (To obtain this report in machine readable form, send e-mail to .)
Вопросы? Предложения? Претензии?
Обсудить материал в моем ЖЖ

|