Вот вам число - самое маленькое решение уравнения:

И его назвали e₀ . Ипсилон ноль. Я не знаю почему так. Наверное, постольку, поскольку у вас возникла проблема с тем как обозначать вещи, ведь до сих пор я использовал нормальные алгебраические записи которые привязаны к w.
Так или иначе, но вы можете видеть, что это невероятная материя! Я не знаю, является ли это математикой, но это очень абстрактно, очень завораживающею. Из всего этого, сделанного Кантором, имелась целая масса замечательных результатов и интересных выводов для чистых математиков. Некоторые люди расценили теорию множеств как болезнь. Пуанкаре, великий французский математик, сказал, что теория множеств это болезнь от которой, он надеется, будущие поколения оправятся. Но другие принялись переделывать всю математику, используя теоретико-множественный подход. В итоге современная топология и многие абстрактные разделы математики XX века оказались в значительной степени результат этого самого теоретико-множественного подхода, который обобщил все.
Математика XIX века была в некотором смысле на качественно более низком уровне, она была больше сосредоточена на решения узких, специальных вопросов и уравнений. Математика же двадцатого столетия (тяжело писать историю математики с тысяча девятисотого года, не заглядывая глубже) была теоретико-множественной. Она опиралась на "структурное" описание своих объектов. Математика девятнадцатого столетия была обеспокоена формулами, возможно бесконечными рядами Тейлора. Но математика двадцатого столетия поднялась на уровень теории множеств.
И в этом была заслуга Кантора. Некоторые люди ненавидят все это, утверждая, что Кантор разрушил и разрушает математику. Он взял конкретную математику и создал что-то очень слабое, к примеру, вместо предметного анализа абстрактный анализ. Другим же людям подход Кантора очень понравилось. В общем, все это было очень спорным.
Все это было крайне спорно. И что подлило масла в огонь - то, что вырисовались некоторые противоречия. И теперь это стало более чем вопрос вкуса. В жизни существуют такие ситуации, когда дело вашей жизни действительно постигла неудача. Когда вы получили очевидную ерунду из всего что сделали. И вот представьте, вы, фактически, получаете очевидную ерунду, чуть ли не из самой теоремы Кантора, которая говорит, что для любого бесконечного множества имеется большее бесконечное множество - множеством всех его подмножеств. Само это утверждение звучит довольно разумно. Это диагональная процедура Кантора (у меня нет времени углубляться в детали).
Но проблема состоит в том, что если вы верите, что для любого бесконечного множества есть множество его подмножеств, то что случаться если вы это примените к универсальному множеству, множеству всех множеств? Проблема в том, что множество всех множеств имеет в себе все множества, но диагональный метод, возможно, дал бы вам большее множество, которое является множеством всех подмножеств всего. В общем, появилась проблема, и эта проблема была замечена Бертраном Расселом.

Бертран Рассел

Кантор, я думаю, вполне возможно тоже заметил эту неприятность, но Бертран Рассела понесло, и он постарался сообщить это всем окружающим, преподнося эти плохие новости каждому! По крайней мере, Гедель приписывал именно Расселу заявление, что имеется глубокий кризис.
Причиной бедствия, которое заметил Рассел - в доказательстве Кантора. Это было множество всех множеств, которое не является членом самого себя и которое, оказывается, является ключевым шагом в доказательстве!
"Множество всех множеств, которые не есть членами самого себя" звучит как вполне разумное определение множества. Но если вы спросите находиться это множество внутри себя или нет, то не зависимо оттого, что вы ответите, вы получите противоречие. Это подобно ложному утверждению. Множество всех множеств, которые не члены самого себя, содержат самих себя тогда, и только тогда, когда не содержит самих себя.
И что это значит?
Или что некоторые способы определения множеств плохи, или универсальное множество вляпало вас в неприятность? Что же не так с "множеством всего"?
С теорией множеств возникли проблемы, и это становилось более и более ясным. Я полагаю, что Рассел поспособствовал тому, что бы проблема была признана каждым. Он помог признать, что мы имеем серьезный кризис в наших методах рассуждений. Методы рассуждений, которые казались на первый взгляд совершенно законными, в некоторых случаях вели к очевидным проблемам и противоречиям. Имеется целое семейство парадоксов, разрекламированных Расселом, например, парадокс Берри. Тот, который я только что изложил, называется парадокс Рассела. Также можно упомянуть другой парадокс - Бурали-Форти (Burali-Forti).
Бесспорный факт, что внимание мира ко многим из этих парадоксов действительно было привлечено Расселом. Рассказывая о парадоксе, Рассел, как водится, ставил сноску, где сообщал, что этот парадокс он обнаружил, когда читал работу Бурали-Форти. Но теперь все называют этот парадокс парадоксом Бурали-Форти. Бурали-Форти, я думаю, на протяжении всей своей оставшейся жизни пытаясь загладить это неожиданное приписывание, потому как не считал, что имеются какие-то неприятности в математике!
Хорошо. И так имеется кризис, и Рассел был одной из ключевых фигур в его центре. Но в этот момент Девид Гильберт приходит на помощь.

Гильберт: Формальный аксиоматический метод.

Гильберт сказал: давайте использовать всю технологию формальной логики изобретением которой тогда занимались многие, и давайте придем к какому-то исключительному максимуму. Поскольку одна из причин, почему мы оказались в затруднении и пришли к парадоксам в математики исходя из теории множеств, состоит в том, что слова человеческой речи очень неопределенные. Поэтому если мы хотим избавиться от этих неприятностей в математике, это, например, надо избавиться от местоимений. К примеру нередко, вы не знаете точно, к чему это местоимение обращается, и это все путает. В математике имеется масса всякого рода вещей, которые на нормальном языке оказываются неопределенными.
Гильберт сказал, что способ избавиться от всех этих проблем - иметь конечный набор аксиом и искусственный язык для механического получения математических утверждений. Это была идея формализма, доведенная до своего логического конца.

Формализм.

Довести формализм до абсолютного предела - это значит изобрести полностью искусственный язык с абсолютно точными правилами игры (искусственной грамматикой и всем остальным) и тогда, возможно, будут устранены все проблемы подобные проблеме Рассела. Это была честолюбивая программа - раз и навсегда водрузить математику на твердый фундамент формализма.
Еще одна вещь, которую Гильберт подчеркивал особо (это было ключевым вкладом сделанным им) состояла, как он полагал, чтобы правила игры для формальной аксиоматической системы математики должны быть настолько точны, что вам остается только механическая проверка любого доказательства. В результате мы будем полностью уверенны действительно ли доказательство объективно и механически подчинено правилам или нет. При этом не должно присутствовать и духа человеческого вмешательства. Не должно иметься ни капли субъективной оценки, ни тени колебаний в интерпретации.
Если кто-то потребует чтобы ему предоставили доказательство, это доказательство должно быть абсолютно ясным, механическим, проверяемым. Должно быть хорошо видно что доказательство повинуется правилам. И тогда станет ясно что вы доказали теорему или это ваши рассуждения содержат ошибку и вы потерпели неудачу.
Вся идея состояла в том, чтобы иметь абсолютно черно-белую математику, точную и абсолютно правильную. И это - традиционное понимание математики.

Черное или Белое?

Реальный мир, который мы знаем представляет собой практически полный бардак. Верно? Во всех своих проявлениях сложный и грязный. Но есть одно место, где сущности должны быть абсолютно ясными. Абсолютно черное или белое можно найти в чистой математике.
Это разновидность того, о чем говорил Гильберт и он предложил этот идеал как цель - иметь полную формализацию математики и устранить все неясности и проблемы. Теперь это стало некой программой. И данное мероприятие, как предполагалось, не было чем-то, что вы делаете за Уик-энд. Гильберт объявил это как перспективную цель, которая закончится торжественным водружением математики на твердый, устойчивый фундамент. И он, включая Джона фон Неймана принялись за работу над этим и некоторое время (в течении тридцати лет) эти планы выглядели вполне обнадеживающе. И вот на этом пути (это беглое резюме столетней работы, поскольку, я уверен, каждый из вас об это знает) появилось несколько проблем.
Проблема 1931 года - Курт Гедель и проблема 1936 года Алан Тьюринг.

1931 Гедель.
1936 Тьюринг.

Они показали, что поставленная цель не могло быть достигнута, что имеются фундаментальные препятствия для полной формализации всей математики и представление ее как черно-белой и абсолютно, кристально ясной. Помните, Гильберт предлагал следующее: мы должны формализовать математику так, что каждый на земном шаре мог бы согласиться с тем, что некоторое доказательство является правильным или неправильным. Правила игры должны быть абсолютно явными. Это должен быть искусственный язык и тогда математика даст вам абсолютную истину. "Абсолютная истина" должна быть выделена очень красивым шрифтом и вы должны слышать пение ангелов в момент произнесения этих слов! За этим скрывалась мысль, что именно мы, математики, владеем абсолютной истиной! Это наше! Никто не имеет ее кроме нас! В этом была идея фикс. Но оказалось, что это не сработало. Почему?
Гедель несколько удивил математиков, показав, почему идея Гильберта не может работать. Это было очень необычно, когда Гедель предложил свое доказательство в 1931 году. А Тьюринг, я думаю, проник в это куда глубже в 1936 году.
Теперь позвольте мне сделать беглое резюме на пять минут, чтобы вскользь показать, что они сделали.
Гедель начинает с конструкции "это утверждение ложно". Что я здесь утверждаю? Ложь? Допустим. Допустим это ложь, но тогда получается, что я говорю правду! И так "это утверждение ложно" является ложным, если и только если оно истинно. Имеется парадокс.
Гедель же рассматривает похожее утверждение "это утверждение недоказуемо"

"Это утверждение недоказуемо"

Это утверждение недоказуемо средствами и из аксиом формальной системы Гильберта. Недоказуемо в пределах системы, которую Гильберт пробовал создать.
Теперь подумайте смысле утверждения, которое говорит, что оно недоказуемо.
Имеется только две возможности. Оно доказуемо или оно недоказуемо. Предполагается, что вы можете заставить это утверждение говорить, что оно недоказуемо, и предполагается, что имеется некоторый способ говорить это на языке системы Гильберта. Для этого потребовались много ума: Геделева нумерация, обманный маневр, чтобы сделать косвенное обращение к самому себе, ведь местоимения "Я" и "Это" не встречаются в математических формулах. Так что все это потребовало большой сообразительности от Геделя. Но основная идея проста - "это утверждение недоказуемо"
И так имеются две возможности. Или доказуемо или нет. Оно доказуемо или нет в системе, которую построил Гильберт для окончательной формализации математики.
Хорошо.
Если оно доказуемо, а утверждение говорит, что оно недоказуемо, то тем самым мы доказываем средствами системы ложное утверждение (доказываем истинность утверждения, которое утверждает что оно недоказуемо - бред!). Это не очень хорошо. Но если оно действительно недоказуемо и оно говорит, что оно недоказуемо, тогда все прекрасно. Это действительно недоказуемо и значит, мы имеем дыру. Вместо доказательства чего-то ложного мы имеем неполноту.
Мы имеем истинное утверждение, доказательство которого нашей системе невозможно, то есть системе не подчиняется (оно же действительно в ней недоказуемо!).
Таким образом, идея состоит в том, что мы или доказываем ложное утверждение, что является для системы ужасным (она противоречива), либо мы имеем что-то не столь ужасное, но все же плохое, потому что в этом случае наша формальная аксиоматическая система неполна. Имеется что-то что истинно, но оно не доказывается в пределах нашей системы. Поэтому мечта об окончательной формализации математики раз и навсегда на этом заканчивает свое существование.

Я не думаю, что Гильберт хотел раз и навсегда формализовать всю математику. Он не говорил, что мы отныне должны работать только на искусственном языке и строить одни только формальные доказательства. Формальные доказательства имеют склонность быть очень длинными и совершенно непригодными для чтения. Я думаю, что цель Гильберта была философской. Если вы по прежнему считаете, что математика выражает абсолютную истину, тогда, как мне кажется, Гильберт должен быть прав, и способ раз и навсегда формализовать математику должен существовать. Это разновидность того, что математические логики и пытались сделать, это то же самое что аксиоматический метод пытался добиться. Это идея разбиения доказательств на все меньшие и меньшие шаги. И Лейбниц думал над этим, и Буль думал об этом, и Фрег, и Пеано, и Рассел, и Уайтхед ломали голову тоже. В этом скрывалась идея: прояснить то, как математики работают шаг за шагом. Прояснить так, что бы это звучало убедительно. К сожалению, эта мечта потерпела крах.
И так все оказались в ужасном положении, придя к этому финалу. Вы читаете эссе Германа Велли (Hermann Weyl) где Джон фон-Нейман высказывает что-то наподобие: я стал математиком, потому что это была моя религия, я верил в абсолютную истину. В ней виделась гармония, в то время как реальный мир был ужасен, но я нашел убежище в теории чисел. И внезапно Гедель приходит и все разрушает. Я готов покончить с собой!
Так что местами все это было ужасно. Однако утверждение…

"Это утверждение недоказуемо"

… выглядит очень вызывающе-странным утверждением.
Но имеется способ рационализации подобных странностей, и люди преуспели в этом необычайно. Вы не хотите стоять лицом к лицу перед неприятной действительностью. И по поводу такой неприятной действительности легко пожать плечами и сказать: ну и что? Это только слова, какие реальные проблемы от этого могут возникнуть? Высказывания, с которыми лично я обычно работаю в математике, совсем не похожи на утверждения такого рода.
Все это - ерунда! Если вы строите подобного вида глупости, значит вы ищите проблемы на свою голову!
Но подобная рационализация заходит слишком далеко. Поскольку Гедель сделал высказывание …

"Это утверждение недоказуемо"

… в терминах элементарной теории чисел.
В своей оригинальной форме это утверждение нонсенс. Когда, кто, где слышал о математической формуле, которая утверждает, что оно недоказуема? Но это факт. Гедель построил такое утверждение в виде высказывания о числах в языке элементарной теории чисел, в арифметике. Это было огромное по размеру утверждение но некоторым хитрым способом используя Геделеву нумерацию всех арифметических утверждений использующих простые числа, он записал это так, чтобы это выгладило как утверждение реальной математики. Оно действительно косвенно ссылалось на себя, и оно действительно говорило, что оно недоказуемо.
Именно поэтому действительно появилась проблема. Но люди действительно не знали, что делать с этим. Я бы сказал, они были не "удивлены", а сверхудивлены, даже скорее шокированы!

1931 год Гедель "это утверждение недоказуемо" поразительно!

Представьте мою реакцию, реакцию юноши, читающего это доказательство. Я конечно слежу за всеми этими рассуждениями шаг за шагом, но мне они не нравиться. Они не вызывает во мне энтузиазма. Конечно, все это справедливо. Но если я скажу, что мне все это нравится, если я скажу, что это замечательно и вполне меня устраивает, то я пойду мимо всего этого дальше и стану молекулярным биологом, организую биотехнологическую компанию и стану богат. Я не стану делать ничего в этой области!
Тут появляется Тьюринг.

1936 год Тьюринг

Теперь я изложу подход Тьюринга. Тьюринг проникает глубже в эту проблему. Тьюринг начинает говорить относительно компьютеров. Это тот самый момент, в который все и произошло!

1936 год Компьютер Тьюринга.

Тьюринг изобрел компьютер только потому, что Гильберт утверждал, что должна иметься механическая процедура, которая разрешает, является ли доказательство правильным или нет. Тьюринг демонстрирует то, что Гильберт в действительности подразумевал. Он показывает, что должна иметься программа для проверки доказательств. Но сначала Тьюринг должен объяснить, что такое компьютер. Это машина Тьюринга и все что ее касается находиться в работе Тьюринга от 1936 года, когда еще не было никаких компьютеров, поэтому это была умозрительная часть его работы. И я просто настаиваю на том, что именно это и был момент изобретения компьютера. Это был компьютер общего назначения, идея которого была изложена именно тогда именно в той работе. Работе изложенной на бумаге.
Тьюринг фактически показал, что имеется осмысленные конкретные утверждения, которые не подвластны влиянию математике. Сейчас мы думаем о компьютерах как о физических устройствах, поэтому они подобны чему-то известному нам в физике. Но та машина, работала бесконечно, была идеализацией и для нее Тьюринг обнаруживает Проблему остановки.

1936 год Компьютер Тьюринга. Проблема остановки.

Проблема остановки утверждает, что не имеется никакого способа разрешить вопрос остановиться ли в конечном итоге любая программа компьютера с любыми данными на входе или нет.
Сейчас вполне очевидно, что вопрос остановки программы компьютера - легчайшая в мире вещь. Вы полностью властвуете над этим, и когда у вас заканчивается терпение или вас беспокоит, что программа слишком долго не хочет останавливаться, а вроде уже пора, вы останавливает процесс. Кому как, а вам некогда больше ждать! Но что показал Тьюринг, так это то, что, если вы не устанавливаете для программы никакого крайнего срока, то возникает проблема.
Это очень абстрактная математика. В реальном мире всегда имеется крайний срок. Вы не можете запустить программу на миллион, миллиард, 10¹⁰¹⁰ лет! Если вы устанавливаете срок, проблема остановки очень легко решается. В принципе вы и только вы управляете программой, которая долго работает. Вы можете наблюдать за ней и видеть, останавливается ли она в заданной точке или нет.
Но Тьюринг показал, что если вы не устанавливаете никаких сроков, тогда нет ни какого другого способа решить эту проблему. Нет никакого способа узнать заранее (вычислить наперед) остановиться ли когда-нибудь та или иная программа компьютера или нет.
Если она останавливается, то вы можете, в конечном счете, обнаружить это по результатам. Проблема же состоит в том, чтобы заранее понять, что ситуация безнадежно и следует прервать выполнение программы.
Не имеется никакой механической процедуры, которая решит заранее остановиться ли данная программа компьютера или нет, ведь если она не остановиться, то следует отказаться от ее запуска вообще. Не существует никакого множества аксиом в смысле Гильберта, опираясь на которые можно было бы доказать остановиться ли программа или нет.
Если бы такая была, вы всегда могли доказать остановиться ли программа или нет. Вы могли бы перечислять все возможные доказательства в порядке их длинны и проверять являются ли очередное высказывание истинным. В конечном счете вы нашли бы доказательство, что данная программа остановится или что она не остановиться. И это дало бы вам метод заранее решить остановиться программа или нет.
На практике перечисление всех возможных доказательств потребует астрономического количества времени. Вообразите, сколько существует доказательств, которые имеют длину всего в одну страницу! Вы никогда, не перечисли ли бы их! Но теоретически, если это Гильбертова формальная аксиоматическая система существовала бы, вы можете пройти все доказательства в порядке их длинны и проверить подчиняются ли они правилам? Отсюда, если вы имеете формальную аксиоматизацию математики, то это вам позволило бы всегда доказать остановиться ли программа или нет, что и будет для вас механической процедурой. Пробегая все возможные доказательства в порядке размера, вы можете решить остановиться ли программа или нет. Но Тьюринг показал, что вы не можете сделать этого. Его доказательство, межу прочим использует диагональный метод Кантора. На самом деле все эти идеи связаны, но у нас нет ни минуты времени, чтобы погружаться в это.
Таким образом, я думаю, что работа Тьюринга устанавливает границы математики и кажется намного естественнее потому, что мы обсуждаем вопрос относительно некого физического устройства - компьютера.

1936 год Компьютер Тьюринга. Проблема остановки в природе.

Пофантазируем слегка. Вы строите этот теоретический компьютер, который может работать без остановки, компьютер который никогда не ломается. Он может иметь так много памяти, сколько вы пожелаете, поэтому если ваши числа станут слишком большими, то для них можно нарастить память тем или иным образом. Это не такая уже и фантазия. Мы имеем устройства подобные этому повсюду. Правильно? Поэтому это звучит намного более конкретно. Ограничения математики, обнаруженные Тьюрингом звучат более серьезно и более опасно, чем те, что найдены Геделем.
Но что же получается? Компьютер был изобретен как аргумент в сумасшедшем теоретическом споре?
Похоже. Ибо вы не увидите упоминаний о миллионах и миллиардах долларов от новых технологий в публикации 1936 года, но там было практически вся эта технология в эмбриональном виде. Как постоянно подчеркивал фон-Нейман: универсальная машина Тьюринга это на самом деле идея программируемого компьютера общего назначения. Конечно, к тому моменту уже имелись машины, которые давно уже делали разные вычисления. Но они делали специальные вычисления. Они были счетными машинами, механическими вычислителями и я еще застал их и даже использовал в юности. Но понятие компьютера - это понятие машины Тьюринга, которая может делать то, что и любая вычислительная машина может делать. В публикации есть все идеи по поводу того что мы называем программным обеспечением: что эта машина общего назначения и это гибкая машина. Так что публикация Тьюринга действительно содержит все необходимое и (как продолжал настаивать фон-Нейман) в ней все изложено очень ясно. В общем, там вы имеете полностью всю технологию!
По существу, публикация Геделя, как я уже говорил, содержит язык ЛИСП в скрытом виде, а работа Тьюринга, учитывая, что там появляется машина Тьюринга, явно содержит машинный язык. Это, на самом деле, очень плохой машинный язык и эта машина - устройство которое ни один человек в здравом уме не захочет программировать. Но Тьюринг хотел представить этот механизм настолько простым, насколько это возможно. Очевидно, что если бы его работа содержала руководство для реального машинного языка, реальной машины, его затея оказалась бы безнадежной. Никто бы не понял его идеи.

Хорошо. Но что случилось со всеми этими идеями дальше? Случилось то что Гильберт умирает, во всю громыхает Вторая Мировая Война, и когда я, юноша, в 50-ых годах читаю эссе Джона фон-Неймана относительно всего этого, то уже становиться ясно, что миром движут куда менее философские идеи. Все покатилось под откос, и вот теперь мы все стали миллиардерами запустив глобальную сеть!
Люди были мало заинтересованы в решении философских проблем и компьютеры превратились в технологию. К этому был привлечен и Тьюринг, и фон-Нейман так же.
Но я, глупый, пытался понять, что же происходило в основаниях математики. На этом пути я увяз где-то на стадии 1930-го года и никак не мог ее преодолеть. Что случилось? Со мной случилось то, что я не мог согласиться с тем, что говорили все, кого это заботило. Теперь, конечно, всем известно, что существует много проблем в жизни помимо математики и гносеологии. Имеются проблемы связанные с семьей, всякие жизненные проблемы, войны, политика поставляет массу проблем, как известно. Но я никак не мог признать то, что о чистой математике говорили сами математики. Они говорили, мол, мы должны делать математику точно так же как делали ее раньше. Но, продолжали они, математика всегда так делалась, поэтому нет никаких проблем в том, что меня, глупого, беспокоит. Это была типичная реакция на результаты Геделя и Тьюринга.
В начале все были шокированы, потом наступило безразличие. Все впали из одной крайности в другую. Все, кого это хоть немного заботило, утверждали, что все это либо очевидно, либо все это несостоятельно. Мол, это не имеет ни какого влияния на то, как мы должны делать математику. Меня это жутко расстраивало. Меня преследовала неполнота и у меня появилась идея.
Когда я был ребенком, я хотел быть физиком, и многие математики говорили, что как физик я никогда не вникну в математику глубоко. Я никогда не преуспею в ней и увязну на подступах! Но я хотел быть физиком и носился с массой своих физических идей. И здесь следует сказать, что в то время как в математике происходили все эти кризисы, параллельно имелся еще один кризис, протекавший уже в физике, который, фактически, начался в 1920-х годах - это квантовая механика. И ключевая дата в нем - 1924 год.

1924 год Квантовая механика.

Это, говоря обобщенно, проблема неопределенности и случайности в фундаментальной физике. В юности, помимо эссе относительно Геделевской теоремы о неполноте, восклицавших "О мой бог!", я читал эссе, которые так же недоуменно спрашивали, что случилось с детерминизмом в физике? Что случилось с предсказуемостью? Может ли быть мир случайным? Бог играет в кости?
Эйнштейн сказал: нет, Бог не играет в кости! Он ненавидел квантовую механику. Но все остальные с ним не соглашались, они признавали, что бог действительно играет в кости.

Бог играет в кости!

Квантовая механика - это наиболее успешная физическая теория когда-либо созданная. Именно она подарила нам транзисторы и компьютеры. Но даже притом, что Эйнштейн внес вклад в развитие квантовой механики, он ненавидел ее. Но Эйнштейн был не прав. Бог действительно играет в кости!
В общем, у меня появилась сумасшедшая идея. Я подумал, что на самом деле проблема в большем, что Гедель с Тьюрингом это только вершина айсберга. Возможно, все намного хуже и возможно мы действительно имеем в чистой математике хаос. Другими словами, случается, что возможная причина, по которой вы не можете что-то там доказать, не в том что вы глупы или вы не достаточно долго пытались добиться успеха, нет. Возможно, причина в том, что там ничего нет! Иногда причина, почему вы не можете решить математическую проблему не в том, что вы недостаточно сильны или не достаточно четко поставлен вопрос, а потому что никакого решения не существует вообще. Возможно, математический вопрос не имеет под собой никакой конструктивной основы. Возможно, за ожидаемым ответом нет никакой связи, закономерности, структуры, которые вы пытаетесь уловить в объектах мира чистой математики. Возможно, причина, почему вы не видите там никакой закономерности, кроется в том, что никакой закономерности или структуры там просто и нет!
Одним из мотивов, побудивших меня так думать, были простые числа. Есть ряд работ о простых числах, которые утверждают, что на распределение простые числа можно смотреть статистически. Создается впечатление, что на их распределение накладывается некоторая хаотичность. И именно с такой точки зрения иногда исследователи пытаются размышлять о простых числах. И это происходит в теории чисел, которая является королевой чистой математики?!
И так, с одной стороны я слышал эти разговоры о вероятностных соображениях по поводу простых чисел, а с другой, относительно бога, играющего в кости в фундаментальной физике, что однозначно проявляется на уровне атомов. И я начинаю думать, что в целом это может быть тем же, что и происходит в основании математики.
Это то, что я вознамерился проверить и этот проект занял у меня много времени. Одним из первых шагов, который стоит сделать в этом направлении, - прояснить, что вы подразумеваете под хаотичностью в математике. Может хаотичность - это то, что вы понимаете под отсутствием структуры? Это отсутствие порядка, отсутстие закономерности?

Хаотичность: отсутствие структуры.

Такое определение, скорее, логическое определение хаотичности, чем статистическое понимание хаоса. Это не то, что мы обычно подразумеваем в физике, где есть случайный физический процесс наподобие подбрасывания монеты. Здесь же я не беспокоюсь, о предсказании, о том что произойдет. Я только смотрю на что-то уже существующее и говорю, имеет ли это структуру, стоит за этим какая-то закономерность или нет? Это логическая или структурная хаотичность в противоположность физической непредсказуемости и хаотичности. Это различные вещи. Очень близко связанные, но различные.
Идея, которую придумал я, придумал независимо и одновременно Колмогоров. Что-либо случайно, если оно не может быть сжато в более короткое описание. Оно максимально хаотично, если по существу вы должны записать это только так, как оно и представлено. Другими словами, нет никакой сокращенной теории, которая может породить то же самое. Например, набор физических данных был бы случаен, если бы единственным способом их издать было бы представление их в виде таблицы. Но если имеется теория, вы сжимаете множество наблюдений в небольшое число физических принципов или законов. И чем больше сжатие, тем лучше теория: в соответствии с принципом бритвы Оккама лучшая теория - самая простая теория. Я бы сказал, что теория это программа. Рей Соломоноф (Ray Solomonoff) сделал некоторые интересные заключения в том же направлении, но для индуктивного вывода. Он не дал определения хаотичности, но она там просматривается. Если вы думаете о теории как о программе, которая вычисляет результаты наблюдений, то чем меньше длинна программы по отношению к ее выходу (который и есть прогноз наблюдения) тем лучше теория.
Между прочим, это тоже что делает аксиоматический подход. Я бы сказал, что в основе аксиоматического подхода лежит та же самая идея. Вы имеете много теорем или математических истин, и вы сжимаете все это в набор аксиом. Теперь, почему это считается хорошим подходом? Потому что в этом случае возникает меньше риска. Аксиомы - это гипотезы, которые вы выдвигаете. Вы вынуждены брать их на веру и при этом рискуете. Вы не доказываете их на основании чего-то там. Вы берете их как данность. И чем меньше вы, таким образом, примете на веру, тем выше безопасность, тем меньше риск ошибиться. И так, чем меньше аксиом вы принимает на веру, тем лучше для вас. Поэтому, сжимая большое количество теорем (из которых и состоит вся теория) в компактный набор аксиом, вы выигрываете в математике так же как в физике.
Хорошо, но что представляет из себя отсутствие структуры или случайность? Вы сначала должны определить это! Если я собираюсь находить отсутствие структуры, отсутствие закономерности в чистой математике, то я должен для начала определить что я под этим подразумеваю. И я хотел бы назвать этот предмет "алгоритмически-информационной теорией". Она имеет дело с алгоритмической информацией. Или вы можете, если вам нравиться, назвать это сложностью, программно-размерной сложностью.

Алгоритмическая информация

Основная идея в том, что вам следует наблюдать за размером самой короткой программы, самой маленькой программы (меня не беспокоит продолжительность ее работы). Это наиболее короткая программа, которая вычисляет кое-что. Размер - это количество бит, которые я должен загрузить в компьютер, чтобы тот выдал мне этот объект. Такая минимальная по размеру программа и есть наиболее короткое алгоритмическое описание этого кое-чего и это то, как я измеряю его сложность, его алгоритмически-информационное содержание или программно-размерную сложность.
Это подобно теории рекурсивных функций: я не забочусь относительно того, сколько времени мне понадобится для вычислений. Все эти рассуждения очень абстрактны! Все это строится в том смысле, что я ищу дополнительные идеи к абстрактным темам 1930-х годов, используя идее измерения размера программ и глядя исключительно на размер программы.
Так что случается, когда вы начинаете наблюдать за размером той или иной программы?
Давайте предположим, что мы находим нечто такое, что самая маленькая программа, вычисляющая это, оказывается такой же длинны, как и сам оригинал. И, предположим, нет никакого способа сжать это. Еще раз: общая идея - смотрите на размер компьютерной программы, и не заботьтесь относительно времени ее выполнения. Если требуется миллиард лет - пускай будет миллиард лет. Меня это нисколько не тревожит! Информация - вот единственная вещь, о которой я думаю. Все сосредоточено на битах информации. На размере компьютерной программы. Хорошо?
Что произойдет, если вы теперь начнете играть с этой идеей и примерять ее к той или иной области исследований? Окажется, что всюду, куда не повернись, вы получаете неполноту и неразрешимость. Вы получаете это самым плохим из всех предполагаемых способом. Например, это случается с первой вещью, которую вы хотите сделать: вы никак не можете решить, что некоторая конкретная цепочка цифр отвечает определению хаотичности. Невозможно! Вы никак не можете вычислить программно-размерную сложность чего-либо! Вы никак не можете определить размер самой маленькой программы для получения этого.
Если вы имеете программу, которая вычисляет что-то, то имеется верхний предел размера такой программы. Размер самого этого "что-то" и является верхним ограничением программно-размерной сложности. Но вы никогда не сможете доказать существование какой-либо минимальной границы. И это мой первый результат неполноты в этой области и, как мне кажется, Джек Шварц (Jack Schwartz) был очень воодушевлен этим. В нормальной, практически полезной теории сложности вычислений, где вас куда больше заботит время выполнения, чем количество бит в программе, нижние ограничения намного тяжелее получить, чем верхние ограничения. Если вы находите для чего-то остроумный алгоритм, вы оказываетесь сверху связанным по времени, которое понадобится для завершения вычислений. Если вы нашли способ сделать это быстрее, вы показали, что это можно сделать быстрее. Но проблема состоит в том, что бы показать, что вы получили самый быстрый из возможных алгоритмов. Это намного тяжелее. Правильно? Хотя это может быть сделано в некоторых случаях для класса некоторых алгоритмов, в целом это крайне сложно.
И так, в алгоритмически-информационной теории вы не можете найти никаких нижних пределов! И я написал статью на этот счет в 1975 году в Scientific American.
Основная идея состоит в том, что вы не можете доказать какие-либо нижние пределы программно-размерной сложности для отдельных объектов. Такова их специфика (даже притом, что большинство из них - это цепочки цифр) они несжимаемы в этом смысле. Они случайны в этом смысле. Им недостает структуры. Оказывается, вы можете легко показать, что большинство объектов удовлетворяют этому определению - не имеют никакой структуры. Если вы посмотрите на произвольную сотню чисел, записанных в виде цепочек цифр, то почти все они не имеют никакой структуры согласно нашему определению. Но вы никогда не можете быть уверены в каждом отдельном случае. Вы не можете доказать это в отдельно взятом случае.
Говоря строго, могут иметься, конечно, много исключений. С N битами аксиом вы можете определить все объекты программно-размерной сложностью до N. Но это все, куда вы можете дойти.
И мой самый плохой результат неполноты, где вы имеете однозначное отсутствие структуры в чистой математике, имеет отношение к числу которое я определил и назвал как "вероятность остановки".

= вероятность остановки

Как это число определено? Очень просто. Тьюринг сказал, что вы не можете решить остановиться ли программа или нет, что нет никакой механической процедуры для определения этого. Но я говорю: давайте рассматривать действительное число, которое являться вероятностью того, что программа полученная наугад, из битов выбранных подбрасыванием монеты, останавливается. Что я получу в итоге, опираясь на Проблему остановки Тьюринга, если я произвожу программу таким образом? Что является вероятностью того, что эта программа остановиться? Факт, что это должно быть действительное число. Оно четко определено, если вы скажете мне (и под этим подпишитесь), что взято в качестве языка программирования.

_computer = вероятность остановки компьютера

Как только вы примете решение, станет конкретным действительным число. Математически это не очень сложная вещь! По сравнению с кардиналами, комплексной математикой, это сравнительно простой объект.
Однако оказывается, что этот объект максимально непостижим!

максимально непостижим

Что это означает, "максимально непостижим"? Мы имеем цепочку цифр или битов, из которых составлено данное действительное число. Как только я устанавливаю компьютер, язык программирования вероятность остановки становится конкретным действительным числом, которое зависит от выбора компьютера и языка программирования, для которого я "написал" программу подбрасывая монету. В результате мы имеем действительным число, и я выписываю его, скажем в двоичном коде в виде цепочки единиц и нулей. Это очень незатейливое определение. Прекрасно! Но оказывается, что эти 1-цы и 0-ли не имеют никакой математической структуры. Они не могут быть сжаты. Для вычисления первых N бит требуется программа в N бит. Чтобы получить первые N-бит надо иметь N бит аксиом. Это не редуцируемая математическая информация. В этом и состоит ключевая идея.

-не редуцируемая информация

Это должна звучать ужасно! "Не редуцируемая математическая информация". Потому что общепринятая идея относительно математики (идея Гильберта) в том, что вся математическая истина может поместиться в небольшой набор аксиом. Классическая идея в том, что мы можем договориться относительно того, что есть "самоочевидным" и надежным. Но если вы хотите определить из каких бит состоит вероятность остановки , то нет никакой возможности уменьшить это до чего-нибудь более простого, чем само это .
имеет математическое определение с довольно простой структурой, если я определил компьютер и язык программирования. Я даже выписал программу на ЛИСПЕ, которая вычисляет это число в слабом смысле. На самом деле вы не можете вычислять это число. Если бы вы могли вычислить это число, то оно не было бы непостижимо! Вы можете получить его как предел сходимости, но оно сходиться очень, очень медленно. Вы никогда не сможете узнать то, насколько вы приблизились к цели. Не существует никакой вычислимой регулярной сходимости. Не существует никакого способа, чтобы выяснить, как долго надо двигаться, чтобы получить первые N правых бита числа . Чтобы получить предел сходимости вы только все больше и больше смотрите на программы из K бит, каждый из которых вносит вклад (1/2) ^K в вероятность остановки:

⁼

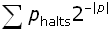
В этом случае вы должны получить первые N бит числа и время нахождения каждого растет подобно самой длинной из возможных конечных программ из N-бит, которая является версией функции "Работящий бобер" (Busy-Beaver function).
Так что же является точным определением ? Напишите программу подбрасыванием монеты для каждого ее бита - каждый бит, получен случайно, независимым броском чистой монеты. Очень важный момент - программа должна быть "саморазграничивающаяся". Компьютер должен считывать у нее каждый бит раз за разом. Каждый раз компьютер должен говорить "я хочу следующий бит программы" и вы бросаете монету. Но компьютер должен решать самостоятельно, что у него уже имеется достаточно бит чтобы получилась целостная программа. Программа должна саморазграичиваться чтобы определить вероятностную меру правильно. Нет никакого маркера, указывающего место, где закончилась программа: программа должна указывать это в пределах самой себя. Для этого нужна уловка, уловка кодирования. Все это техническая проблема, чтобы сделать вероятность четко определенной. Но все это - специальный технический момент в моей теории.
И так это вещественное число в пределах от 0 до 1. Это вероятность того, что программа, каждый бит которой произведен независимым подбрасыванием справедливой монеты, в конечном счете остановится. Я устанавливаю язык программирования, выбираю универсальную машину Тьюринга (Universal Turing Machine и это отмечено индексом) и получаю _UTM -вероятность остановки специфической универсальной машины Тьюринга. И я фактически выбираю специфическую UTM, которую я программирую, допустим, на ЛИСП-е (только что бы обрисовать идею). Но вы могли бы делать это с любой универсальной машиной Тьюринга, на которой саморазграничивающаяся программа могла бы работать.
И так максимально непостижимое число. Это тот случай, где математическая истина не имеет никакой структуры или формы и это то, что мы никогда не сможем и не собираемся узнать! Позвольте уточнить, что я здесь получил. То, что я имею - это максимальная хаотичность (подобно независимому подбрасыванию справедливой монеты) в чистой математике. Фактически, я могу получить это в элементарной теории чисел, подобно тому, как это делал Гедель. Я могу определять биты числа из диафантовых уравнений.
Точкой опоры здесь будет вот что. Вы имеете простой математический вопрос о том, чем будет каждый конкретный бит числа :

Первый бит 1 или 0?
Второй бит 1 или 0?
Третий бит 1 или 0?
...

Но эти ответы не имеют никакой структуры. Они напоминают подбрасывание монеты. И это притом, что каждый ответ - строго математический ответ о математическом объекте. Ответ об определенных битах определенного вещественного числа, которые обязательно должны быть 1-й или 0-м. Фактически, мы никогда не сможем этого знать и это моя версия независимого подбрасывания монеты в математике. Даже если бы вы знали все четные биты в числе , это не поможет вам получить любой из нечетных битов. Если бы вы знали бы первый миллион бит, это не поможет вам получить следующий. Это действительно напоминает независимое подбрасывание чистой монеты. Это максимально хаотично, это имеет максимальную энтропию.
Физики чувствуют себя вполне уверенно с хаотичностью, но здесь мы рассматриваем черно-белый мир чистой математики. Как в нем такое возможно? Как это может быть? Каждый из этих битов однозначен. Это или однозначно 0 или однозначно 1 потому что - определенное вещественное число. Это станет однозначным, как только я устанавливаю универсальную машину Тьюринга или язык программирования, с которым я имею дело. Но, оказывается, правильно думать относительно каждого бита, что он не "черное" или "белое", не 0 или 1, а что здесь все так хорошо уравновешено, так изящно сбалансировано, что это "серое"!
Имеется еще один способ представить это.
Давайте вернемся к Лейбницу. Что является главной идеей математики? Классическая идея состоит в том, что если кое-что существует, то этому есть причина. Лейбниц! Если что-то истинно, то это истинно по некоторой причине. Теперь в чистой математике причиной истинности чего-либо является доказательств и работающий математик ищет доказательство, ищет причину того, что это утверждение истинно. Но биты числа или 0, или 1 тоже являются математической истиной, которая оказывается истиной без всякой причины, они истины случайно! И именно поэтому мы никогда не будем знать, что это за биты.
Другими словами дело не в том, что Гильберт был немного не прав. Дело не в том, что классические представления о математике - немного неверны, что в монолите математической истины имеется несколько мелких прорех, что имеются отдельные вырожденные случаи типа "Это утверждение недоказуемо". Нет, все не так! Все намного хуже! Имеются обширные области, где математическая истина не имеет никакой структуры вообще, где все максимально непостижимо, где все полностью случайно, где вы получаете математическую истину подобно подбрасыванию монеты, где истины случайны, где есть истины без всякой причины. Именно поэтому вы никогда не можете доказать являются отдельные биты числа 0-ми или 1-ами. Потому что нет никакой причины отдельный бит считать 0-м или 1-ей! Именно поэтому вы не можете разыскать никакого доказательства. Другими словами это так изящно сбалансировано, является ли каждая частица 0-ем или 1-ей, что мы никогда не сможем этого узнать.
В общем, не только Гильберт был не прав, поскольку Гедель и Тьюринг показали…, я хочу обобщить все это. На Геделя, после того как он получил неполноту, смотрели удивленно. Удивляло, что никакой конечный набор аксиом не может содержать всю математическую истину. Неполнота Тьюринга выглядит несколько более естественной. Но с моим подходом, когда вы рассматриваете размер необходимой программы, я сказал бы, что все это выглядит неизбежным. Везде, куда вы не повернетесь, вы сталкиваетесь с каменной стеной, и неполнота смотрит вам в лицо.

Программно-размерная сложность & & не редуцируемая информация     => делает неполноту неизбежной.

Это то над чем я работал. Теперь какова реакция остального мира на эту мою работу? Справедливо было бы сказать, что единственные люди, которым понравилась моя работа - это физики. Это не удивительно, потому что идея пришла из физики. Я продвигаю свою странную идею, которую именую хаотичностью, которую приношу в логику, и чувства логиков восстают против нее. У вас есть представления о размере программы, программно-размерной сложности, что-то типа энтропии в термодинамике. Поэтому физики находят это вполне удовлетворительным, потому что они рассматривают это как идеи из их области, но вторгающиеся в логику. Но логикам это очень сильно не нравиться.
Я думаю, что у этой неприязни могут иметься политические причины, но, скорее всего, в основе ее лежат концептуальные мотивы. Идеи относительно хаотичности настолько чужеродны математике и логике, что это становится для нее просто кошмаром! Это - самый жуткий кошмар, который сбывается! Я думаю, что они предпочли бы просто не думать относительно всего этого.
С другой стороны физики заключают, что эти идеи восхитительны. Поскольку они хорошо помнят кризис, который они миновали в 1920-х годах по поводу все той же хаотичности в основаниях физики. И они говорят, что это постигло не только нас, мы не единственные кто сталкивается с хаотичностью. Оказывается, чистые математики сталкивается с ней тоже! Они ничем не лучше нас!
Я приведу пример отношения физиков к моей теории. Случилось так, что только на этой неделе я нашел эту статью. Существует английский журнал New Scientist который выходит каждую неделю. Он подобен английской версии Scientific American за исключением того, что он немного более яркий, он несколько более забавный и выходит каждую неделю. И в последнем выпуске (тот, что вышел 26-го февраля, следующий еще не вышел) на обложке представлена статья "Случайная Реальность". Если вы откроете издание и посмотрите на статью, то она посвящена работе двух физиков, очень спекулятивной (гипотетической) работе. Они пробуют представить как наше пространство и время, наше трех- или четырехмерное пространство-время, наш мир, появляется из первоначального случайного субстрата.
Посмотрите эту статью, если не сложно. На моем сайте имеется ссылка на нее. "Случайная Реальность". Или найдите этот журнал New Scientist.
Причина, почему я упоминаю эту работу, в том, что авторы утверждают, что их работа была вдохновлена Геделем и моей работой на границах логики. Они пробуют осознать этот материал. Они говорят, что физики были заинтересованы результатами Геделя, но они не могли прикоснуться к этому, потому что все это выражено не в терминах физики. Но моя работа, говорят они, имеет смысл в физике! В этом нет ничего удивительно, - я и почерпнул свою идею из чистой физики! Эти идеи обрело для них смысл, потому что вышла из их области и возвращается туда же.
Фактически, они вообще не используют мои определения и мои теоремы. Так как меня просили оценить их работу, я вынужден был сказать, что это действительно не имеет никакого отношения ко мне. Мой материал упомянут в предисловии потому, что моя работа помогла стимулировать их исследование. Но их работа находится в области физики и не имеет никакого отношения к моей области, области алгоритмической информационной теории.
Но я полагаю, это интересный пример того, как сумасшедшие идеи имеют иногда неожиданные последствия. Я уже говорил, что формальные системы не преуспели в моделировании рассуждений, но они прекрасно преуспели в вычислениях. В итоге идеи Гильберта все же имел ослепительный, мировой успех, но как технология, а не как эпистемология.
И вот, неожиданно появились физики, которые заинтересовался моими идеями программно-размерной сложности. Они рассматривают все это по-другому, от термодинамики и энтропии. Кроме того, имеются еще некоторые работы физиков по поводу демона Максвелла, так же использующие мои идеи. Я упоминаю это для тех из вас, кто имеет некоторые базовые представления о физике.
Но я должен заметить, что философы не подняли брошенный им шар. Я думаю, что логики ненавидят мою работу. Они не переваривают ее! Я для них что-то типа порнографии - выгляжу неприличным предметом в мире чистой логики. Ведь мои результаты настолько отвратительны!
Вот вам в сущности и вся моя история.
В заключении позвольте вам порекомендовать посмертное собрание эссе И. Берлина "Власть идей" (Isaiah Berlin The Power of Ideas), которое только что была издано. Более чем сто лет назад немецкий поэт Гейне предупреждал французов о том, чтобы они не недооценивать власть идей: "философские концепции, которые профессора лелеют в тиши, могут уничтожить цивилизацию". Поэтому, полагал он, остерегайтесь идей, и я думаю это справедливое предупреждение.
Идея Гильберта достигнуть предела формализации математики возникла по эпистемологическим причинам. Это была попытка разрешить философское проблемы и противоречия в основаниях математики. В процессе развития этот проект потерпел крах, как я уже объяснял, из-за работ Геделя и Тьюринга. Но благодаря всем этим усилиям мы имеем полностью формализованные компьютеры, программные языки для них, которые теперь используются повсюду. Они обеспечивают меня доходом, они вероятно обеспечивают вас доходом… В конце концов это Школа Информатики, и она тоже результат всего этого, правильно? Мы находимся здесь благодаря этим идеям!
Идеи заработали!
В другом смысле, конечно, но заработали превосходно!
Поэтому я люблю приносить извинения несколько агрессивным способом относительно своей области исследований. Я люблю говорить, что моя область не имеет никакого применения, что наиболее интересная вещь в моей области программно-размерной сложности как раз и состоит в том, что это не может быть никак применено! Поскольку вы не можете вычислить размер самой маленькой программы. Но это то, что завораживает в этих идеях, потому что это указывает пределы того, что мы можем постичь. Именно поэтому программно-размерная сложность имеет только эпистемологическое применение.
Говоря более серьезно, я думаю, что мораль истории в том, что глубокие идеи не имеют быстрого дохода в долларах, но иногда они имеют неожиданные и значительные последствия. Я никогда не ожидал увидеть, что два физика используют мой материал способом, каким они это делают в "Случайной Реальности". Кто же может знать?!
Истина в том, что компьютер обеспечивают нас прибылью, но я думаю, что так же истина и в том, что имеется масса прекрасных, непрактичных идей. Иногда, когда идея так красива…

Я имел здесь прекрасную беседу с вашими людьми. Питер Ли за завтраком сказал мне, что эти идеи настолько красивы, что они наверняка истины! И главное не упустить их! Те самые опасные непрактичные идеи, они могут преобразовывать наше общество. Некоторая простая идея относительно сети, например, соединила в Сеть мир! Или идея относительно существования полностью искусственных языков, исключительно дял того чтобы механически увидеть они означают….
Это очень опасные идеи!
Очень!
Большое спасибо за внимание!


Библиография

1. G.J. chaitin, Algorithmic Information Theory, Cambridge University Press, 1987.
2. G.J. chaitin, Information, Randomness & Incompleteness, World Scientific, 1987.
3. G.J. chaitin, Information, Randomness & Incompleteness, 2nd Ed., World Scientific, 1990.
4. G.J. chaitin, Information-Theoretic Incompleteness, World Scientific, 1992.
5. G.J. chaitin, The Limits of Mathematics, Springer-Verlag, 1998.
6. G.J. chaitin, The Unknowable, Springer-Verlag, 1999.
7. I've recently finished programming my entire theory in LISP. This will eventually be my book Algorithmic Information Theory in LISP, in preparation.

Вопросы? Предложения? Претензии?
Обсудить материал в моем ЖЖ